Задача 32538 ...

sova

2019-01-04 19:05:47

★

4a)
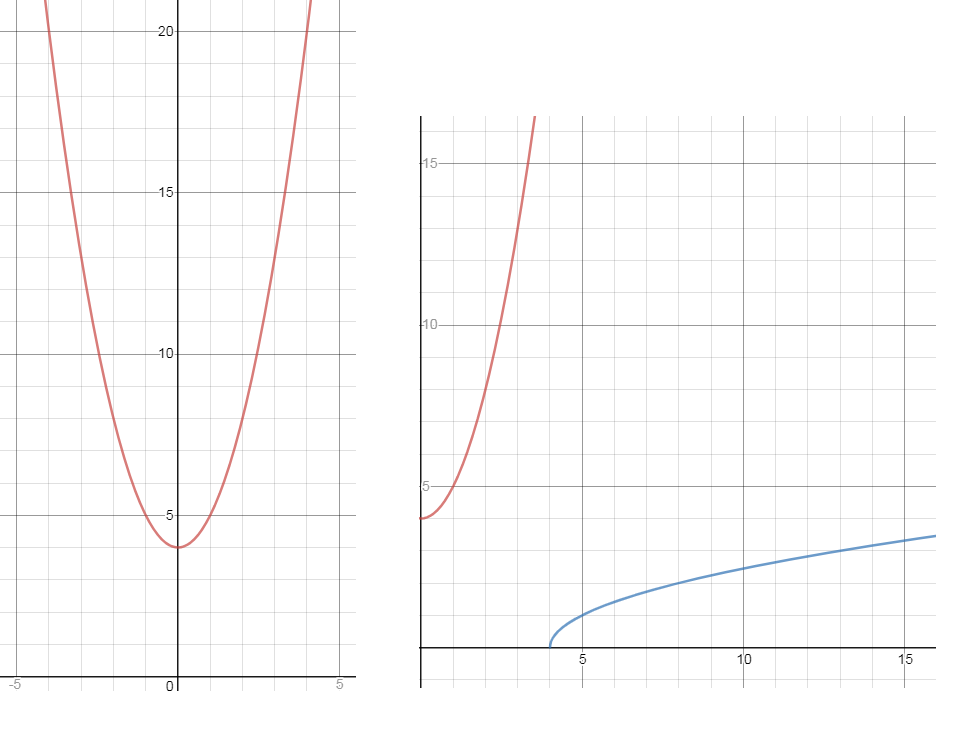
y=x^2+4
f(x)=x^2+4
D(f)=(- ∞ ;+ ∞)
Е(f)=[4;+ ∞ ) ( график парабола, наименьшее значение при х=0 равно 4)

Чтобы составить обратную функцию,
меняем х и у местами

х=у^2+4 ⇒ y^2=x-4 ⇒ y=± sqrt(x-4)

y=x^2+4 на[b] [0;+∞ )[/b] имеет обратную функцию y=sqrt(x-4)

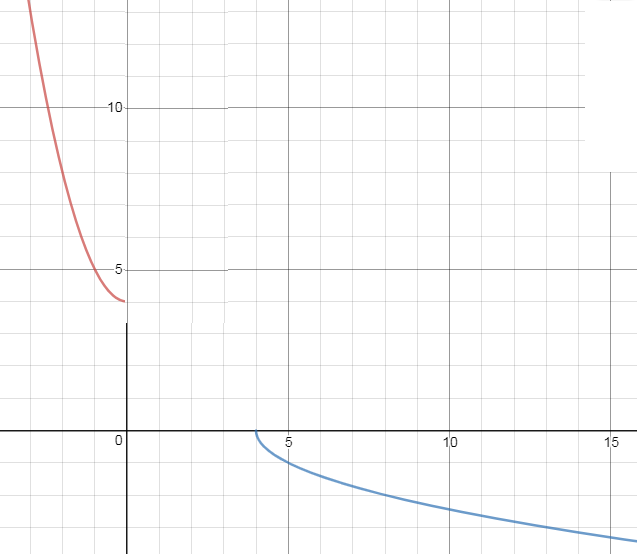
y=x^2+4 на [b]( - ∞; 0)[/b] имеет обратную функцию y= - sqrt(x-4)


Обратная функция f^(-1)=sqrt(x-4)
D(f^(-1))=E(f)=[4;+ ∞ )
E(f^(-1)=D(f)=[0 ;+ ∞ )

Обратная функция f^(-1)= - sqrt(x-4)
D(f^(-1))=E(f)=[4;+ ∞ )
E(f^(-1)=D(f)=(- ∞; 0 )

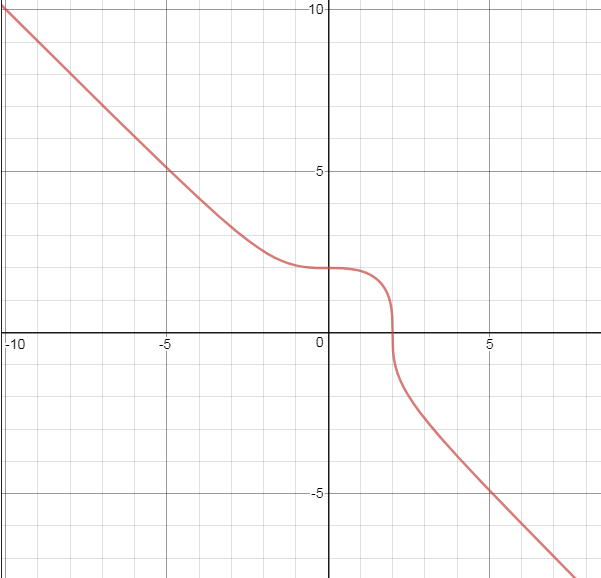
4б)

D(f)=(- ∞ ;+ ∞ )
E(f)=(- ∞ :+ ∞)

Чтобы составить обратную функцию,
меняем х и у местами

x=∛(8-y^3)
x^3=8-y^3
y^3=8-x^3
y=∛(8-x^3)-

f^(-1)=∛(8-x^3)

f=f^(-1)