Задача 32500 ...

vk344135258

29 декабря 2018 г. в 20:00

Задание 3 Найти интервалы непрерывности функции и точки разрыва. Построить график функции

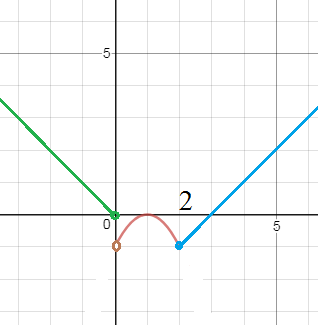
3.4. f(x) =
{ –x, x ≤ 0,
{ –(x – 1)², 0 < x < 2.
{ х — 3, x ≥ 2.

sova

30 декабря 2018 г. в 11:04

★

Функция непрерывна на (– ∞ ;0); на (0;2) и на (2;+ ∞ )
так как
функция y= – x непрерывна на (– ∞ ;0)
функция y= – (x – 1) ² непрерывна на (0 ;2)
функция y= (x – 3) непрерывна на (2; +∞ )

Исследуем точку
х=0
Находим
предел слева
f(–0)=lim_x→–0(–x)=0
предел справа
f(+0)=lim_x→+0(–(x–1)²)= – 1
Предел слева не равен пределу справа, функция не имеет предела в точке х=0, точка х=0 – точка разрыва первого рода.
Скачок
f(+0) – f(–0) = –1 – 0 = – 1 ( функция в точке разрыва первого рода имеет конечный скачок)

Исследуем точку
х=2
Находим
предел слева
f(2–0)=lim_{x→2 – 0}(–(x–1)²)= –1
предел справа
f(2+0)=lim_x→2+0(x–3)= – 1
Предел слева равен пределу справа, функция имеет предел в точке х=2,
f(2)=2–3=–1
предел в точке х=2 равен значению функции в точке х=2
lim_x→2f(x)=f(2)
точка х=2 – точка непрерывности.