Задача 32453 ...
Условие
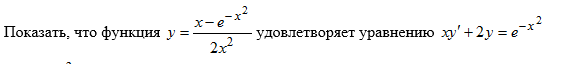
математика ВУЗ
842
Решение
★
=((1-e^(-x^2)*(-x^2)`)*2x^2-4x*(x-e^(-x^2)))/(4x^4)=
=((1-e^(-x^2)*(-2x))*2x^2-4x*(x-e^(-x^2)))/(4x^4)=
=(2x^2+4x^3e^(-x^2)-4x^2+4x*e^(-x^2))/(4x^4)=
=(2x^2e^(-x^2)-x+2e^(-x^2))/(2x^3)
Подставляем в уравнение:
(2x^2e^(-x^2)-x+2e^(-x^2))/(2x^2)+2*(x-e^(-x^2))/(2x^2)=e^(-x^2);
неверно.
Не является?
