Задача 32409 Требуется: 1) построить на плоскости XOY...

vk444734150

2018-12-24 23:15:19

Требуется:
1) построить на плоскости XOY область интегрирования заданного интервала;
2) изменить порядок интегрирования и вычислить площадь области при заданном
и при измененном порядках интегрирования.

sova

2018-12-25 09:35:55

★

А

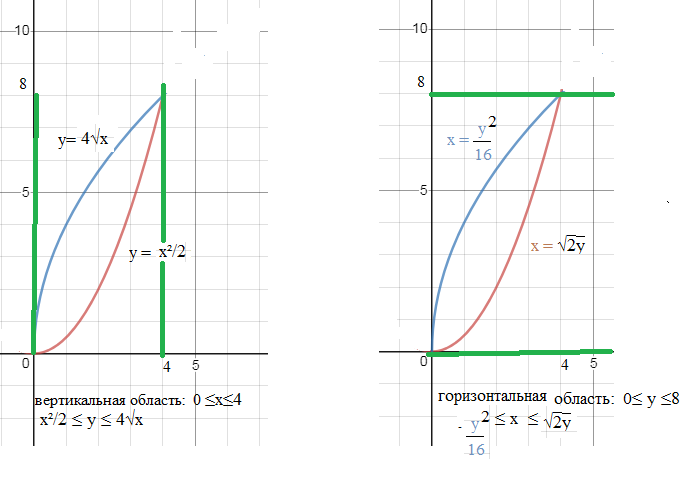
Дано. Вертикальная область интегрирования
0 ≤ x ≤ 4; x^2/2 ≤ y ≤ 4sqrt(x)

Полоса, ограничена [b] вертикальными[/b]прямыми
x=0 и х=4
и кривыми
y=x^2/2 и y=4sqrt(x)

Cм. рисунок слева

Рисунок справа, [b]горизонтальная[/b] полоса , ограничена прямыми
у =0 и у= 8
и уравнения кривых получим из данных уравнений, выразим х через у
y=x^2/2 ⇒ 2y=x^2 ⇒ x=sqrt(2y)
y=4sqrt(x) ⇒ y^2=16x ⇒ x=(1/16)y^2

О т в е т. ∫ ^(8)_(0)dy ∫ ^(sqrt(2y)_(y^2/16)dx

S= ∫^(4)_(0)dx ∫ ^(4sqrt(x))_(x^2/2)dy=

= ∫^(4)_(0)y|^(4sqrt(x))_(x^2/2)dx=

=∫^(4)_(0)(4sqrt(x)-(x^2/2))dx=

=4x^(3/2)/(3/2)|^(4)_(0)- (x^3/6)|^(4)_(0)=

=(8/3)*4^(3/2)-(4^3/6)=(64/3)-(64/6)=64/6=32/3


S= ∫ ^(8)_(0)dy ∫ ^(sqrt(2y)_(y^2/16)dx=

=∫ ^(8)_(0) x|^(sqrt(2y)_(y^2/16)dy=

=∫ ^(8)_(0) (sqrt(2y)- (y^2/16))dy=

=sqrt(2)(y^(3/2)/(3/2))|^(8)_(0) - (y^3/48)|^(8)_(0)=

=(2sqrt(2)/3)*8^(3/2)-(512/48)=

=(2sqrt(2)/3)*16sqrt(2)-(32/3)=

=(64/3)-(32/3)=32/3