Задача 32368 ...
Условие
2.1 y = sin 2x, x₀ = π/4;
2.2 √x − √y = √a, x₀ = 4a;
2.3 { x = e^−3t, y = e^8t, t₀ = 1.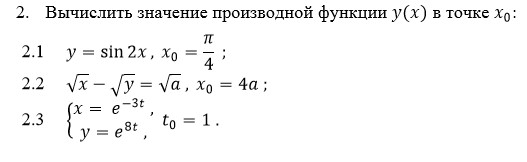
математика 10-11 класс
600
Решение
★
y`=(cos2x)*(2x)`=2cos2x
y`(π/4)=2cos(π/2)=2*0=0
2.2
(sqrt(x)-sqrt(y))`=(sqrt(a))`
1/(2sqrt(x)) - (1/2sqrt(y))*y`=0
y`=sqrt(y)/sqrt(x)
x_(o)=4a ⇒ sqrt(4a)-sqrt(y_(o))=sqrt(a)
y_(o)=a
y`(x_(o);y_(o))=sqrt(a)/sqrt(4a)=1/2
2.3
{x`_(t)=-3e^(-3t)
{y`_(t)=8e^(8t)
y`_(x)=y`_(t)/x`_(t)=8e^(8t)/(-3e^(-3t))=-(8/3)e^(11t)
y`_(x)(1)=(-8/3)e^(11)
