Задача 32361 ...
Условие
6.1 y = 1/(2 - e^(2x));
6.2 y = √(arcsin2x);
6.3 y = sin(lg(x/2)).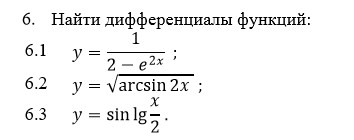
математика 10-11 класс
675
Решение
★
Найти производные и приписать справа dx
1)
f(x)=(2-e^(2x))^(-1)
f `(x)=-1*(2-e^(2x))^(-2)*(2-e^(2x))`
f `(x)=-1*(2-e^(2x))^(-2)*(-e^(2x))*(2x)`
f `(x)=-1*(2-e^(2x))^(-2)*(-e^(2x))*(2)
f `(x)=2*e^(2x)/(2-e^(2x))^(2)
df=2*e^(2x)dx/(2-e^(2x))^(2)
2)
f`(x)=(1/2sqrt(arcsinx))*(arcsinx)`
f`(x)=(1/2sqrt(arcsinx))*(1/sqrt(1-x^2))
df=dx/(2sqrt(arcsinx)*sqrt(1-x^2))
3)
f `(x)=coslg(x/2) * (lg(x/2))`
f `(x)=coslg(x/2) * (ln10/(x/2))*(x/2)`
f `(x)=coslg(x/2) * (ln10/(x/2))*(1/2)
f `(x)=(coslg(x/2))*(ln10) /(x)
df=(coslg(x/2))*(ln10)dx /(x)
