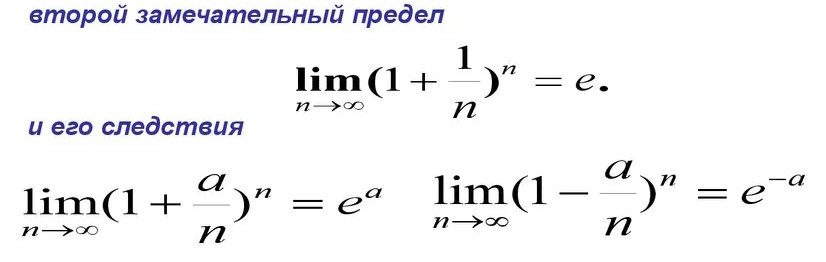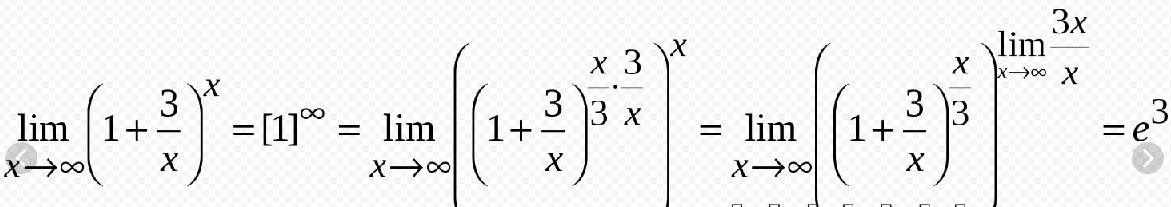Задача 32232 ...

sova

2018-12-21 19:10:39

((x-2)/(x+3))^(3x+5)=((x-2)/(x+3))^(3x)*((x-2)/(x+3))^5

lim_(x→∞)((x-2)/(x+3))^(3x+5)=lim_(x→∞)((x-2)/(x+3))^(3x)*((x-2)/(x+3))^5=
предел произведения равен произведению пределов:
=lim_(x→∞)((x-2)/(x+3))^(3x) * lim_(x→∞)((x-2)/(x+3))^(5)

Cчитаем каждый предел:
lim_(x→∞)((x-2)/(x+3))^(5)=1^(5)=1

lim_(x→∞)((x-2)/(x+3))^(3x)= неопределенность 1^(∞)
применяем второй замечательный предел
делим числитель и знаменатель на х

lim_(x→∞)((1-(2/х))/(1+(3/х)))^(3x)=

= lim_(x→∞)((1-(2/x)^(-x/2))^(-6)/ lim_(x→∞)((1+(3/x)^(x/3))^9=

=e^(-6)/e^(9)=e^(-15)=1/e^(15)

О т в е т. 1/e^(15)