Задача 31699 В основании прямой призмы АВСА1В1С1...
Условие
математика 10-11 класс
10390
Решение
★
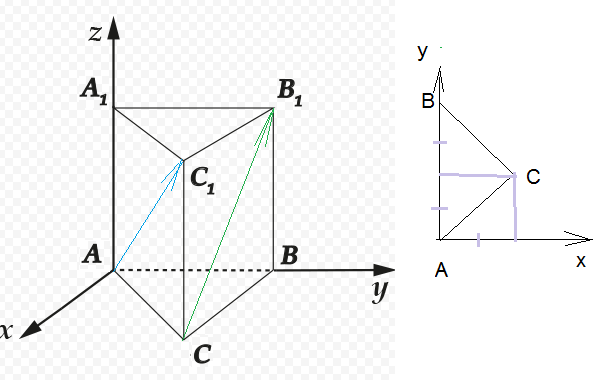
Δ АВС - прямоугольный равнобедренный
A(0;0;0); B(0;8sqrt(2);0); C(4sqrt(2);4sqrt(2);0);
A_(1)(0;0;6); B_(1)(0;8sqrt(2);6); C_(1)(4sqrt(2);4sqrt(2);6)
vector{AC_(1)}=(4sqrt(2);4sqrt(2);6) ⇒ |vector{AC_(1)}|=sqrt(132)
vector{CB_(1)}=(-4sqrt(2);4sqrt(2);6)⇒ |vector{CB_(1)}|=sqrt(132)
cos ∠( vector{AC_(1)},vector{CB_(1)})=(vector{AC_(1)}*vector{CB_(1)})/(|vector{AC_(1)}|*|vector{CB_(1)}|)=
=(-32+32+36)/132=3/11
∠( vector{AC_(1)},vector{CB_(1)})=arccos(3/11)