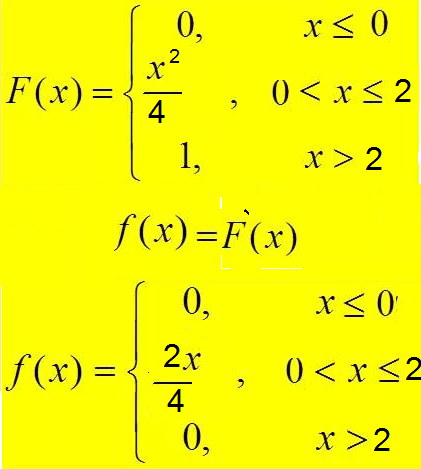Задача 31636 ...
Условие
[m] F(x) = \begin{cases} 0, & x \leq 0 \\ \frac{x^2}{4}, & 0 < x \leq 2 \\ 1, & x > 2 \end{cases} [/m]
Найти f(x), M(X), D(X), σ(X), вероятность попадания НСВ X в интервал [0,5; 1]
Решение
М (Х) = ∫ ^(+ ∞)_(- ∞ )xf(x)dx= ∫ ^(0)_(- ∞ )x*0dx+ ∫ ^(2)_(0 )x*(2x/4)dx+ ∫ ^(+ ∞)_(2)x*0dx=
= 0+ ∫ ^(2)_(0 )(x^2dx/2) + 0=(x^3/6)|^(2)_(0)=8/6=4/3
D(X)= ∫ ^(+ ∞)_(- ∞ )(x - M(X))^2*f(x)dx = ∫ ^(0)_(- ∞ )(x-(3/4))^2*0dx+ ∫ ^(2)_(0 )(x-(3/4))^2*(2x/4)dx+ ∫ ^(+ ∞)_(2)(x-(3/4))^2*0dx=
=0 +∫ ^(2)_(0 )((x^3/2)-(3/4)x^2+(9/32)x)dx + 0=
=((x^4/8)-(3/4)(x^3/3)+(9x^2/64))|^2_(0)=
=2 - 2 + 9/16=9/16
P(0,5 ≤ X ≤ 1)= F(1) - F (0,5)= (1/4)- ((0,5)^2/4)= (1/4)-(1/16)=3/16