Задача 31588 1+y'+y+xy' = 0 y ''' =...
Условие
y ''' = cosx-2x
y''-4y'+20y=0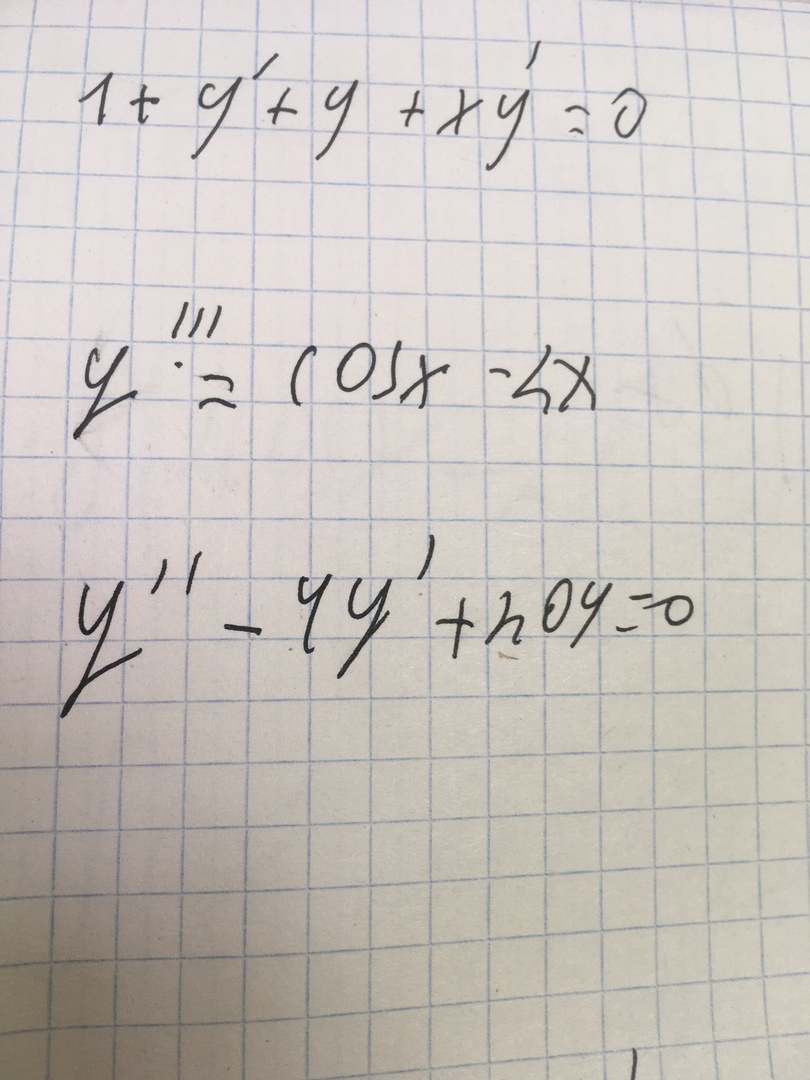
математика 10-11 класс
1126
Решение
★
dy/(1+y)=-dx/(1+x)
∫ dy/(1+y)= -∫ dx/(1+x)
ln|1+y|=-ln|1+x|+lnC
1+y=C/(1+x) - о т в е т
y``= ∫ y```(x)dx= ∫ (cosx - 2x)dx = sinx - x^2 + C_(1)
y`= ∫ y``(x)dx= ∫ ( sinx - x^2 + C_(1))dx= -cosx - (x^3/6) +C_(1)x+ C_(2)
y= ∫ y`(x)dx = ∫ ( -cosx - (x^3/6) +C_(1)x+ C_(2))dx=
= -sinx - (x^4/24)+C_(1)x^2/2 + C_(2)x+ C_(3)
Характеристическое уравнение:
k^2-4y+204=0
D=(-4)^2-4*204=-800
k_(1)=(4- i*20sqrt(2))/2=2-i*10sqrt(2)
k_(2)=(4+ i*20sqrt(2))/2=2+i*10sqrt(2)
Общее решение имеет вид ( см. таблицу)
y=e^(2x)*(C_(1)cos(10sqrt(2))x+C_(2)sin(10sqrt(2)x)
