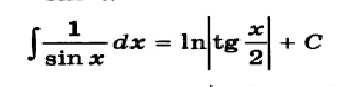Задача 31472 Надо решить 5,8,12 Помогите хотябы с...

vk228823533

2018-12-02 06:18:14

Надо решить 5,8,12
Помогите хотябы с одним или двумя примерами, вы очень сильно поможете

sova

2018-12-03 12:03:59

12.
Линейное неоднородное второго порядка с постоянными коэффициентами.
Решаем линейное однородное
y``+y=0
Составляем характеристическое:
k^2+1=0
k= ± i
y_(общее одн.)=С_(1)cosx+C_(2)sinx

Решаем неоднородное методом вариации произвольных постоянных.
y=С_(1)(x)cosx+C_(2)(x)sinx

Для нахождения С_(1)(x) и C_(2)(x) составляем систему:
{ С`_(1)(x)*y_(1)(x)+ C`_(2)(x)*y_(2)(x)=0
{ С`_(1)(x)*y`_(1)(x)+ C`_(2)(x)*y`_(2)(x)=f(x)

y(1)(x)=cosx ⇒ y`_(1)(x)=-sinx
y(2)(x)=sinx ⇒ y`_(2)(x)=cosx

{ С`_(1)(x)*cosx+ C`_(2)(x)*sinx=0
{ С`_(1)(x)*(-sinx)+ C`_(2)(x)*cosx= - ctg^2x

Решаем систему линейных уравнений относительно
C`_(1)(x) и C`_(2)(x) методом Крамера


Δ=cosx*cosx-(-sinx)*sinx=cos^2x+sin^2x=1
Δ_(1)=cosx*(-ctg^2x)-sinx*0 = - cos^32x/sin^2x
Δ_(2)=0*cosx-(-ctg^2x)*sinx = cos^2x/sinx

C`_(1)(x) = Δ_(1)/ Δ = - cos^3x/sin^2x
C`_(2)(x) = Δ_(2)/ Δ = cos^2x/sinx


Интегрируем
С_(1)(х)= - ∫ cos^3xdx/sin^2x= - ∫ cosx*(1-sin^2x)dx/sin^2x=

= - ∫ cosxdx/sin^2x + ∫ cosxdx = - ∫ d(sinx)/sin^2x + sinx + c_(1)=

=(1/sinx)+sinx+c_(1)

С_(2)(х)= ∫ cos^2xdx/sinx= ∫ (1-sin^2x)dx/sinx = ∫ dx/sinx - ∫ sinxdx=

=ln|tg(x/2)|+ cosx+c_(2)

О т в е т. y=((1/sinx)+sinx+c_(1))*cosx+(ln|tg(x/2)|+ cosx+c_(2))*sinx

=c_(1)cosx + c_(2)sinx + (cosx/sinx)+2sinx*cosx + sinx*ln|tg(x/2))