Задача 3146 На рисунке изображены график функции...
Условие
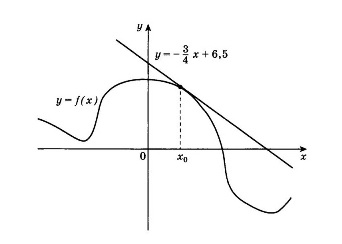
математика 10-11 класс
65529
Решение
★
То есть у′ = (4f(x)-3)′ = 4f′(х) - 0 = 4f′(x) в точке Х0.
Вспомним, что f′(х0) равно коэффициенту при х в уравнении касательной у = (-3/4)х + 6,5 к графику функции f(x) в точке х0.
Значит f(x0) = -3/4. Подставим это значение в у′:
у′ = 4f′(x0) = 4 * (-3/4) = -3 - это и есть искомое значение производной функции y= 4f(x)-3 в точке Х0.
Ответ: -3