Задача 31363 ...

vk139470119

2018-11-28 10:14:48

15.
а) Решите уравнение cos(2x - 3π/2) + sin 4x = 0.
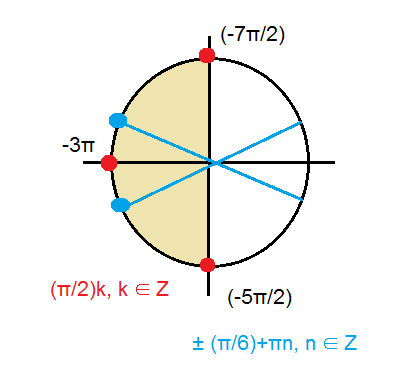
б) Укажите корни этого уравнения, принадлежащие отрезку [-7π/2, -5π/2].

16. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 7.

sova

2018-11-28 14:50:24

15.
cos(2x-(3π/2))=cos(3π/2)-2x)=-sin2x

sin4x=2sin2x*cos2x

-sin2x+2sin2x*cos2x=0

sin2x*(-1+2cos2x)=0

sin2x=0 ⇒ 2x=πk, k ∈ Z ⇒ x=(π/2)k, k ∈ Z

ИЛИ

cos2x=1/2 ⇒ 2x= ± (π/3)+2πn, n ∈ Z ⇒ x= ± (π/6)+πn, n ∈ Z
О т в е т.
а)(π/2)k, k ∈ Z ; ± (π/6)+πn, n ∈ Z

б) -(5π/2); (-3π);(-7π/2)
(-π/6) -3π=-19π/6
(π/6) -3π=-17π/6
корни принадлежащие указанному отрезку.
См. рис.