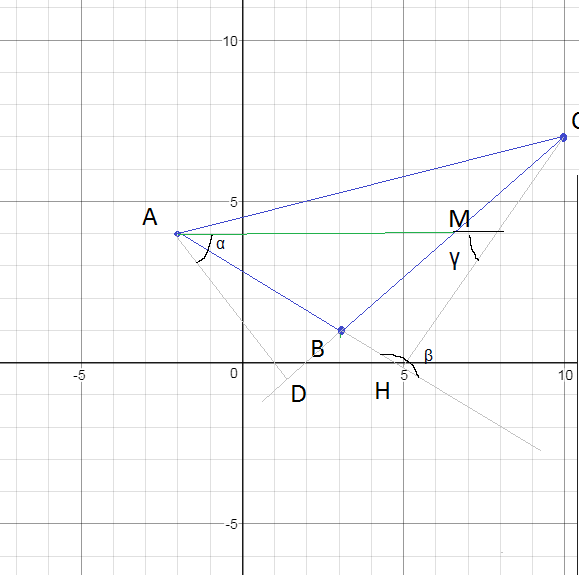
Задача 30967 Даны вершины треугольника ABC: A(-2,4);...

vk496982376

12 ноября 2018 г. в 20:04

Даны вершины треугольника ABC: A(–2,4); B(3,1); C(10,7). Найти: 1) точку P пересечения медианы AM и высоты CH; 2) угол между медианой AM и высотой AD.

sova

12 ноября 2018 г. в 20:45

1.
а)
x_M=(x_B+x_C)/2=(3+10)/2=6,5
y_M=(y_B+y_C)/2=(1+7)/2=4

A(–2;4) M(6,5;4)
Уравнение прямой АМ: y=4

Уравнение прямой AВ:
(x–x_A)/(x_B–x_A)= (y–y_A)/(y_B–y_A)

(x–(–2))/(3–(–2))=(y–4)/(1–4)
(x+2)/5=(y–4)/(–3)
–3·(x+2)=5·(y–4)
–3x–6–5y+20=0
3х+5у–14=0
у=–(3/5)х +(14/5)
k_AB=–3/5
СН⊥АВ
k_AB·k_CH=–1 ⇒ k_CH=–1/k_AB=5/3

y=(5/3)x + m
Прямая проходит через точку С(10;7)
7=(5/3)·10+m
m=–29/3

y=(5/3)x–(29/3) – уравнение СН

При y=4
4=(5/3)·x–(29/3)
x=41/5
(41/5;4) – точка пересечения медианы АМ и высоты СН.

б)
Уравнение прямой ВС:
(x–x_B)/(x_C–x_B)= (y–y_B)/(y_C–y_B)

(x–3)/(10–3)=(y–1)/(7–1)

(х–3)/7=(у–1)/6
6·(х–3)=7·(у–1)
6х–7у–11=0 – уравнение ВС
y=(6/7)x–(11/7)
k_BC=6/7
AD ⊥ BC
k_AD=–7/6
y=(–7/6)x+n
Подставляем координаты точки А
4=(–7/6)·2+n
n=19/3
y=(–7/6)x+(19/3)

⇒
tg β =–7/6; β – угол, который образует прямая y=(–7/6)x+(19/3) c положительным направлением оси Ох

Медиана АМ || оси Ох.
Значит, угол между медианой и высотой равен 180^o– β

α =arctg(7/6)