Задача 30963 ...
Условие
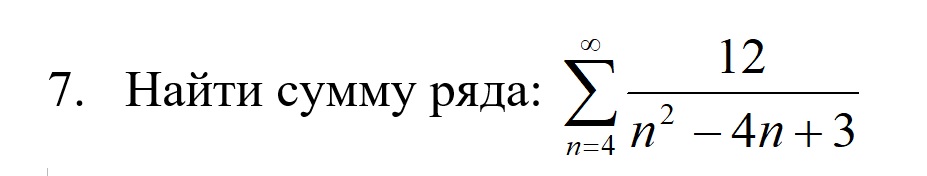
математика ВУЗ
1277
Решение
★
12/(n^2-4n+3)= A/(n-1) + B/(n-3)
12=А*(n-3) + B*(n-1)
A+B=0
-3A-B=12
B=6;
A=-6
Тогда
a_(4)=(-6/3)+(6/1)
a_(5)=(-6/4)+(6/2)
a_(6)=(-6/5)+(6/3
а_(7)=(-6/6)+(6/4)
а_(8)=(-6/7)+(6/5)
...
a_(n)=-6/(n-1) + 6/(n-3)
Складываем
S_(n)=(6/1) +( 6/2)+ (-6/(n-2))-6/(n-1)-6/(n)
S=lim_(n→ ∞ )S_(n)=9
О т в е т. 9