Задача 30961 ...

alekseevadaria

2018-11-12 17:50:19

Вычислить двойной интеграл:

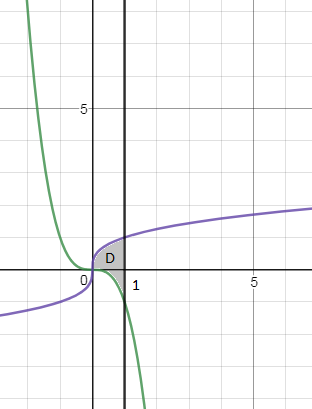
∫ ∫ (8xy+9x^2*y^2)dxdy, где D: x=1, y=-x^3, y=∛x

sova

2018-11-12 18:35:45

★

D: 0 < x < 1; -x^3 < y < ∛x

∫ ∫ (8xy+9x^2·y^2)dxdy= ∫^(1) _(0) (∫ ^(∛x)_(-x^3)((8xy+9x^2·y^2)dy)dx=

= ∫^(1) _(0)( (8xy^2/2)+(9x^2y^3/3))| ^(∛x)_(-x^3)dx=



=∫^(1) _(0)( (4x*(x^2/3)-4*x*x^6+(3x^2*x)+3x^2*x^(9))dx=

= ∫^(1) _(0)( (4x^(5/3)-4*x^7+3x^3+3x^(11))dx=

=(4*x^(8/3)/(8/3) -4*x^(8)/8 +3x^(4)/4 +3x^(12)/12)|^(1)_(0)=

=32/3 -(1/2) +(3/4)+(1/4)= (32/3)+(1/2)=65/3
О т в е т 65/3.