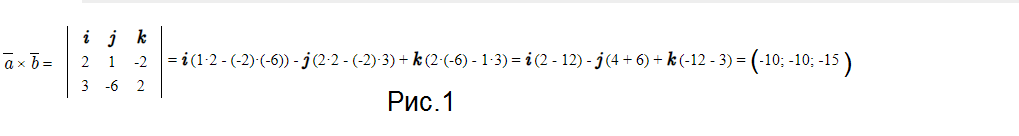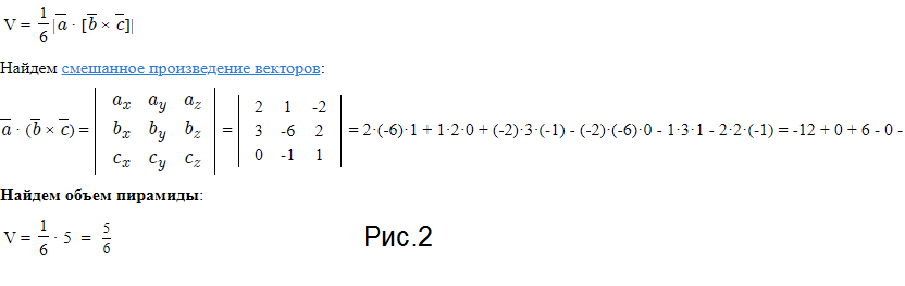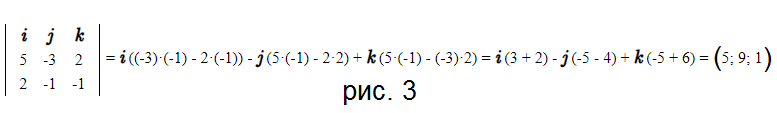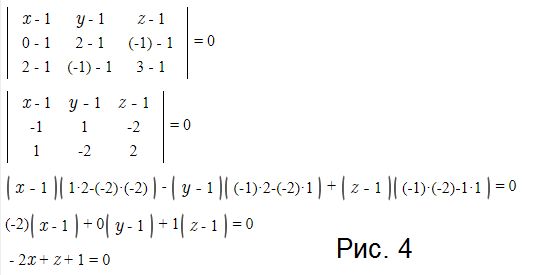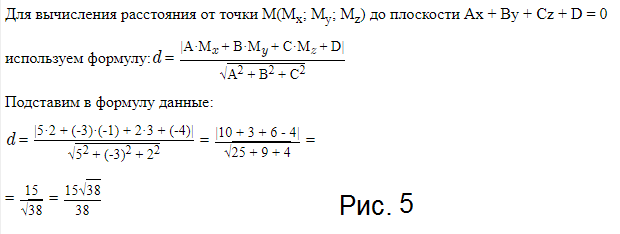Задача 30932 3... 4. . Даны уравнения плоскостей...
Условие
4. . Даны уравнения плоскостей P1: 5 х - 3у +2z - 5 = О,
Р2: 2х-у- z-1 = 0 и координаты точек Mi(l;l;l), М2(0;2;-1), М^(2;-1;3). Найти: а) уравнение плоскости Р3, проходящей через точку М, и параллельной плоскости Pi;
б) уравнение плоскости Р4, проходящей через точку М2 и перпендикулярной плоскостям P1 и Р2;
в) уравнение плоскости P5, проходящей через точки М1 М2, М3;
г) угол между плоскостями Pi и Р2;
д) расстояние от точки М3 до плоскости Р3;
е) общее уравнение прямой L задано уравнениями плоскостей P1 и Р2, написать каноническое и параметрические уравнения прямой;
ж) уравнение прямой L, проходящей через точку М2 и параллельной прямой L;
з) расстояние от точки М3 до прямой L

Решение
a)
Cкалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат.
vector{a}*vector{b}=2*3+1*(-6)+(-2)*2=6-6-4=-4
б)
(2*vector{a}-3*vector{b})*(vector{a}+2*vector{b})=
=2*vector{a}*vector{a}-3*vector{b}*vector{a}+4*vector{a}*vector{b}-6*vector{b}*vector{b}=
=2*(2*2+1*1+(-2)*(-2))-3(-4)+4*(-4)-6*(3*3+(-6)*(-6)+2*2)=
=2*9+12-16-49= - 35
в) Площадь параллелограмма, построенного на векторах, равна модулю векторного произведения.
( см. рис.1)
S=|*vector{a}×vector{b}|=sqrt((-10)^2+(-10)^2+(-15)^2)=sqrt(425)
г) Объем призмы равен модулю смешанного произведения векторов.
Смешанное произведение равно определителю третьего порядка, составленному из координат данных векторов. ( cм. рис.2)
4.
а)
A*(x-x_(1))+B*(y-y_(1))+C*(z-z_(1))=0 - уравнение плоскости, проходящей через точку M_(1) и имеющей нормальный вектор
vector{n}=(A;B;C)
P_(1) и Р_(3) параллельны. Значит их нормальные векторы совпадают.
Нормальный вектор плоскости Р_(1):
vector{n_(1)}=(5;-3;2)
Р_(3): 5*(x-1)-3*(y-1)+2*(z-1)=0
Р_(3): 5х -3у+2z-4=0
б) Нормальный вектор плоскости Р_(4) ортогонален
vector{n_(1)}=(5;-3;2) и vector{n_(2)}=(2;-1;-1)
vector{n_(4)}=vector{n_(1)}×vector{n_(2)}=(5;9;1)
(cм. рис.3)
A*(x-x_(2))+B*(y-y_(2))+C*(z-z_(2))=0 - уравнение плоскости, проходящей через точку M_(2) и имеющей нормальный вектор
vector{n}=(A;B;C)
P_(4):5*(x-0)+9*(y-2)+1*(z+1)=0
5x+9y+z-17=0
в)
P_(5) - уравнение плоскости, проходящей через три точки.
Пусть M(x;y;z) - произвольная точка плоскости.
Тогда векторы
vector{M_(1)M}; vector{M_(1)M_(2)}; vector{M_(1)M_(3)} [b] компланарны[/b].
Условие компланарности - равенство 0 определителя третьего порядка составленного из координат данных векторов. см. рис. 4
г) угол между плоскостями P_(1) и P_(2) - угол между нормальными векторами vector{n_(1)} и vector{n_(2)}
cos ∠ (vector{n_(1)},vector{n_(2)})=vector{n_(1)} * vector{n_(2)}/( |vector{n_(1)}|*|vector{n_(2)}|)=(5*2+(-3)*(-1)+2*(-1))/sqrt(5^2+(-3)^2+2^2)*sqrt(2^2+(-1)^2+(-1)^2)=6/(sqrt(38)*sqrt(6)) =sqrt(3/19)
∠ (vector{n_(1)},vector{n_(2)})=arccso(sqrt(3/19))
д) Расстояние от точки M_(3) До плоскости Р_(3) находим по формуле ( cм. рис.5)
е) Находим общую точку плоскостей.
Пусть х=0
{-3y+2z-5=0
{-y-z-1=0
Умножаем второе уравнение на 2 и складываем с первым
-5у-7=0 ⇒ у=-1,4
z=-y-1=1,4-1=0,4
Направляющий вектор прямой - ортогонален векторам vector{n_(1)} и vector{n_(2)}
Это вектор vector{n_(4)}=vector{n_(1)}×vector{n_(2)}=(5;9;1) ( см. б)
M_(o)(0;-1,4;0,4) - точка принадлежащая прямой L
Уравнение прямой L- как уравнение прямой, проходящей через точку с заданным направляющим вектором.
(x-0)/5=(y+1,4)/9=(z-0,4)/1 - каноническое
Параметризуем:
(x-0)/5=(y+1,4)/9=(z-0,4)/1 = t
Параметрические уравнения:
{x=5t;
{y=9t-1,4
{z=t+0,4
ж)
Прямая L_(1) имеет тот же направляющий вектор, что и прямая L
Уравнение прямой L_(1) как уравнение прямой проходящей через точку с заданным направляющим вектором.
(x-0)/5=(у-2)/9=(z+1)/1
з) См. рис. 6