Задача 30785 ...

vk284880949

5 ноября 2018 г. в 19:56

2. Найдите двузначное число, которое меньше суммы квадратов его цифр на 11 и больше их удвоенного произведения на 5.

4. Построить график функции: y = |х+2|/(4–х²).

5. Решите в целых числах уравнение (х + 1)(y² – х² – 4) = х².

sova

5 ноября 2018 г. в 20:45

2. Двузначное число ab=10a+b
Сумма квадратов его цифр
a²+b²
По первому условию
10a+b+11=a²+b²
По второму условию
10a+b–5=2ab

Система
{ 10a+b+11=a²+b²
{10a+b–5=2ab⇒ 10a+b=5+2ab
a²+b²=2ab+5+11
(a–b)²=16
a–b=4 Или a–b=–4

a–b=–4 ⇒ a+4=b
a=1; b=5
15 – двузначное число о котором спрашивают.

4.
Раскрываем знак модуля:
при x ≥ – 2
|x+2|= x+2
y=(x+2)/(4–x²)
4–x²=(2–x)(2+x)
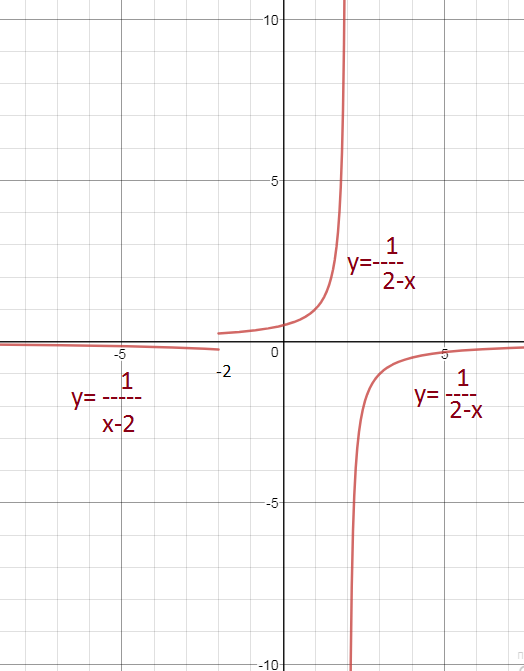
y=1/(2–x)

при x< – 2
|x+2|= – x– 2
y=(x+2)/(4–x²)
4–x²=(2–x)(2+x)
y=–1/(2–x)
y=1/(x–2)

Строим две гиперболы.
Одну y=1/(x–2) при x < –2
Вторую y=1/(2–x) при х ≥ –2

5.
Слева произведение и справа произведение.
x²=1·x²
или x²=x·x

Но x+1 ≠ x

Только так: либо
x+1=x² нет решений в целых числах
(y²–x²–4)=1

либо

x+1=1⇒ х=0
(y²–x²–4)=x² ⇒ y²–4=0 ⇒ y= ± 2

О т в е т. (0;–2);(0;2)