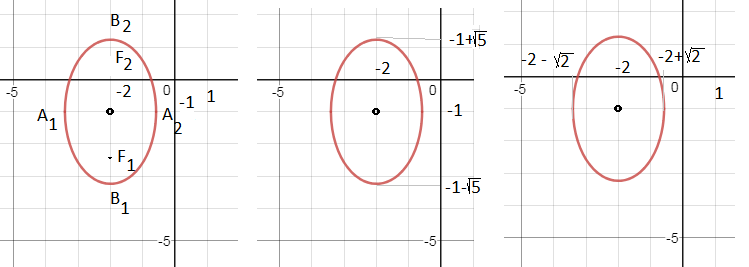
Задача 30776 С помощью выделения полного квадрата...

dashokkkk

2018-11-04 23:58:37

С помощью выделения полного квадрата привести заданное уравнение кривой второго порядка к каноническому виду. Определить тип кривой, найти ее полуоси, эксцентриситет, координаты вершин и фокусов, уравнения директрис и асимптот (если они имеются). Сделать чертеж.

5x^2+20x+2y^2+4y+12 = 0

sova

2018-11-05 09:32:36

★

(5x^2+20x)+(2y^2+4y)+12=0;
5*(x^2+4x+4)-20+2*(x^2+2y+1)-2+12=0
5*(x+4)^2+2*(y+1)^2=10
((x+4)^2/2)+((y+1)^2/5)=1 - каноническое уравнение эллипса
со смещенным центром
центр в точке (-2;-1)
полуоси

b=sqrt(2)
a=sqrt(5)
Значит
с^2=a^2-b^2=5-2=3
с=sqrt(3)

Координаты фокусов:
F_(1) ( -2; -1-sqrt(3)) и F_(2)(-2;-1+sqrt(3))

Эксцентриситет
ε=c/a=sqrt(3)/sqrt(5)=sqrt(3/5)

Координаты вершин
A_(1)(-1; -2-sqrt(2))
A_(2)(-1;-2+sqrt(2))
B_(1)(-2;-1-sqrt(5))
B_(2)(-2;-1+sqrt(5))