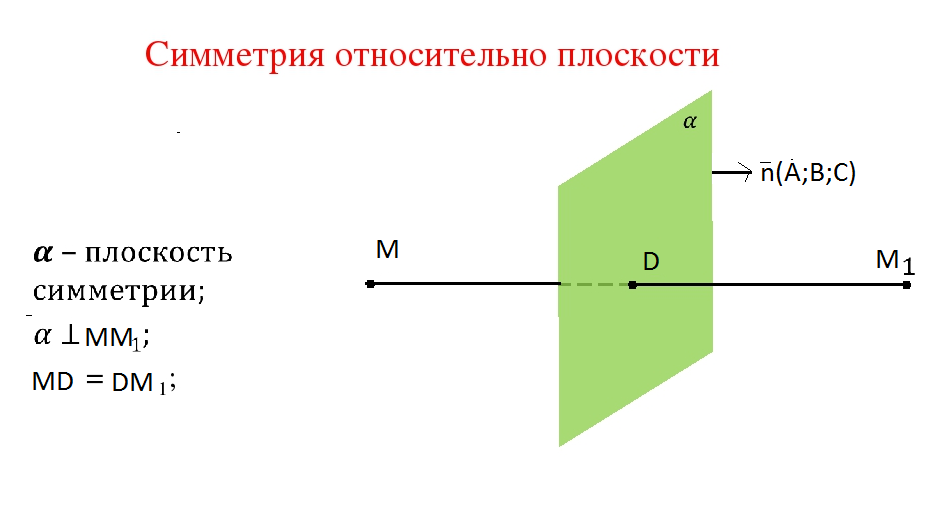
Задача 30775 Найти точку M1, симметричную точке M(1;...

dashokkkk

2018-11-04 22:51:28

Найти точку M1, симметричную точке M(1; 0; 1) относительно плоскости 4x+6y+4z-25 = 0

sova

2018-11-04 23:17:02

Расстояние от точки M до плоскости:
d=|4*1+6*0+4*1-25|/sqrt(4^2+6^2+4^2)=|-17|/sqrt(68)=sqrt(17)/2

Уравнение прямой, проходящей через точку M с направляющим вектором, равным нормальному вектору данной плоскости
vector{n}=(4;6;4):

(х-1)/4=(y-0)/6=(z-1)/4

Находим точку пересечения прямой MM_(1) и данной плоскости
{4x+6y+4z-25=0;
{(x-1)/4=y/6 ⇒ y=(3/2)(x-1)
{(x-1)/4=(z-1)/4 ⇒ z=x

4x+6*(3/2)(x-1)+4*x -25=0
17x=34
x=2
y=(3/2)*(2-1)
y=(3/2)
z=2

Обозначим D(2;(3/2);2)

Составим уравнение сферы с центром в точке D и радиусом d:
(x-2)^2+(y-(3/2))^2+(z-2)^2=17/4

Найдем координаты точки M_(1) - точки пересечения сферы и прямой MM_(1):
{(x-2)^2+(y-(3/2))^2+(z-2)^2=17/4
{y=(3/2)(x-1)
{z=x

(x-2)^2+((3/2)x-3)^2+(x-2)^2=17/4

2x^2-8x+8+(9/4)x^2-9x+9=17/4

(17/4)x^2-17x+51/4=0
x^2-4x+3=0
D=16-12=4
x_(1)=(4-2)/2=1 или х_(2)=(4+2)/2=3
y_(1)=0 или y_(2)=3
z_(1)=1 или z_(2)=3

О т в е т. M_(1)(3;3;3)