Задача 30756 а) Решите уравнение sin^22x+sin^24x =...

slava191

3 ноября 2018 г. в 13:55

а) Решите уравнение sin²2x+sin²4x = 1–(cos(2x))/cos(3x)

б) Укажите корни этого уравнения, принадлежащие отрезку [–π/3; π] (L 13)

sova

3 ноября 2018 г. в 16:13

★

Применяем формулу:
sin² α =(1 – cos2α)/2.

(1 – сos4x)/2 + (1 – cos8x)/2= 1– cos(2x)/(cos3x)

–(cos4x)/2 – (cos8x)/2=–(cos2x)/(cos3x)

(cos4x+cos8x)·cos3x =2cos2x

По формуле
cosα + cos β = 2·cos((1/2)·( α + β)) · cos ((1/2)·( α – β )

2·cos6x · cos (–2x)= 2cos2x

В силу четности косинуса
cos(–2x)=cos2x

2·cos6x·cos2x·cos3x = 2·cos2x

2·cos6x·cos2x·cos3x – 2·cos2x =0

2cos2x·(cos6x·cos3x–1)=0

cos2x = 0 ⇒ 2x= (π/2) + π·n, n ∈ Z ⇒ x = (π/4) + (π/2)·n, n ∈ Z

или

cos6x·cos3x – 1 = 0 ⇒ cos6x·cos3x = 1 ⇒

В силу ограниченности косинуса:
|cosα| ≤ 1 произведение косинусов равно 1, когда оба равны 1 или оба равны (–1):

{cos6x=1 ⇒ 6х=2π·k, k ∈ Z ⇒ х=(2π/6)·k, k ∈ Z
{cos3x=1 ⇒ 3x =2π·m, m ∈ Z ⇒ х=(2π/3)·m, m ∈ Z
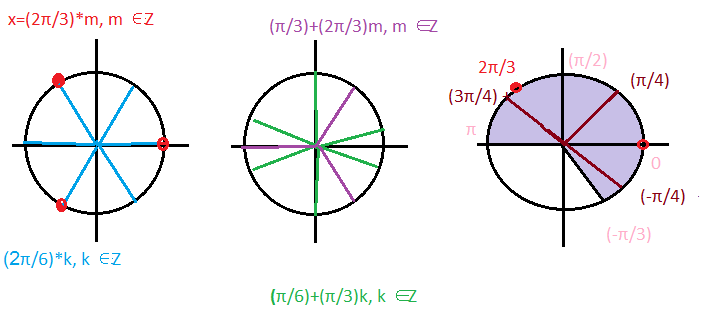
Решение системы х=(2π/3)·m, m ∈ Z (см. рис.1)

или

{cos6x=–1 ⇒ 6х=π+ 2π·k, k ∈ Z ⇒ х=(π/6)+(π/3)·k, k ∈ Z
{cos3x=–1 ⇒ 3x =π+ 2π·m, m ∈ Z ⇒ х=(π/3)+(2π/3)·m, m ∈ Z
Cистема не имеет решений. ( см. рис.2)

О т в е т. (π/4) + (π/2)·n; (2π/3)·m, m,n ∈ Z

б)
Указанному отрезку принадлежат корни:
(–π/4); (π/4); (3π/4)
0; 2π/3