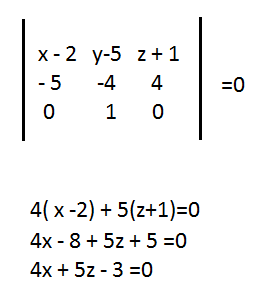Задача 30717 Составить уравнение плоскости,...

krutoyperec

2018-11-01 19:34:17

Составить уравнение плоскости, проходящей через точки A(2, 5, -1), B(-3, 1, 3) параллельно оси Oy.

sova

2018-11-01 19:56:39

Пусть M- произвольная точка плоскости.
Векторы
vector{AM}=(x-2;y-5;z-(-1))=(x-2;y-5;z+1)
vector{AB}=(-3-2;1-5;3-(-1))=(-5;-4;4)
и направляющий вектор оси Оу
vector{j}=(0;1;0)
компланарны.

Условие компланарности - равенство нулю определителя третьего порядка.