Задача 30684 РЕШИТЕ ПОЖАЛУЙСТА , ГДЕ ПРОНУМЕРОВАНЫ...
Условие
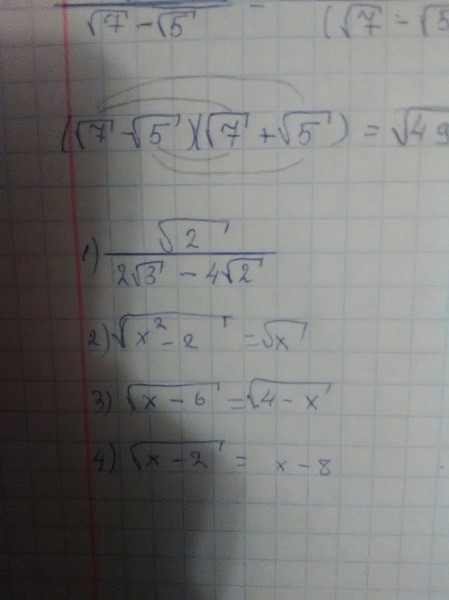
Все решения
=sqrt(2)*(sqrt(2)*sqrt(3)-4)=sqrt(2)*(sqrt(6)-4);
О т в е т. 1/(sqrt(6)-4) можно перевести иррациональность в числитель. Для этого умножаем и числитель и знаменатель на
(sqrt(6)+4)
Получим (sqrt(6)+4)/(sqrt(6))^2-4^2)= -(1/10)*(sqrt(6)+4);
2) ОДЗ
{x^2-2 ≥ 0 ⇒ x ≤ - sqrt(2) или x ≥ sqrt(2)
{x ≥ 0
⇒ x ∈ [sqrt(2);+ ∞ )
Возводим в квадрат:
x^2-2=x
x^2-x-2=0
D=1-4*(-2)=9
x=(1-3)/2=-1 не принадлежит ОДЗ или x=(1+3)/2= 2 принадлежит
О т в е т. 2
в)
ОДЗ
{x-6 ≥ 0 ⇒ x ≥ 6
{4-x ≥ 0 ⇒ x ≤ 4
Система не имеет решений.
Уравнение не имеет корней.
г)
ОДЗ
{x-2 ≥ 0 ⇒ x ≥2
{x - 8 ≥ 0 ⇒ x ≥ 8
x ∈ [8;+ ∞ )
Возводим обе части
x-2=x-8
0*х=-6 - уравнение не имеет корней.
