Задача 30680 Решите неравенство(на...
Условие
(1/9)^(2x+2 / x+4) * 18^(2x)*3x^(-2) ...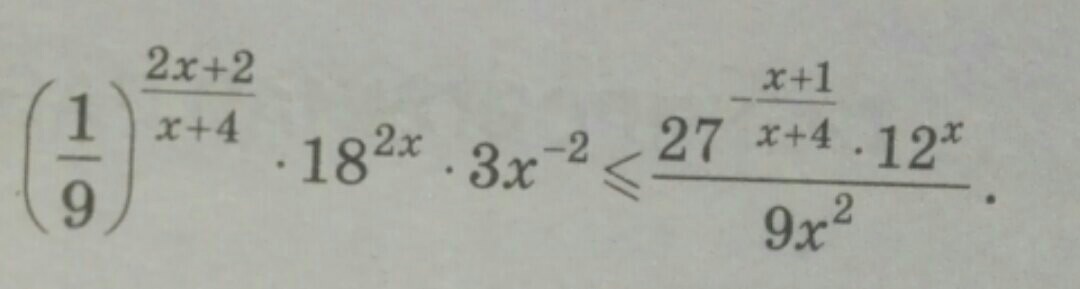
Решение
(1/9)^((2x+2)/(x+4))=3^(-4*(x+1)/(x+4))
18^(2x)=(3^2*2)=3^(2*2x)*2^(2x)=3^(4x)*2^(2x)
(27)^((x+1)/(x+4))=3^(3*(x+1)/(x+4))
12^(x)=3^(x)*4^(x)=3^(x)*2^(2x)
2^(2x) > 0 при любом х
x^2 > 0 при любом х ≠ 0
Умножаем обе части неравенства на x^2/(2^(2x))
3^(4x -4*(x+1)/(x+4) + 1) ≤ 3^(3*(x+1)/(x+4) + x - 2)
Основание 3 > 1, показательная функция возрастает, большему значению функции соответствует большее значение аргумента ⇒
4x -4*(x+1)/(x+4) + 1 ≤ 3*(x+1)/(x+4) + x - 2;
(x+1)*(3-(7/(x+4))) ≤ 0
(x+1)*(3x-12-7)/(x+4) ≤ 0
(x+1)(3x-19)/(x+4) ≤ 0
_-__ (-4) ____+___ [-1] __-_ (0) __-_______ [19/3] __+__
О т в е т. (- ∞ ;-4) U[-1;0) U(0;19/3]
