Задача 30650 Решите систему...
Условие
system{x+y=Pi/4; tgxtgy=5-2sqrt(6)}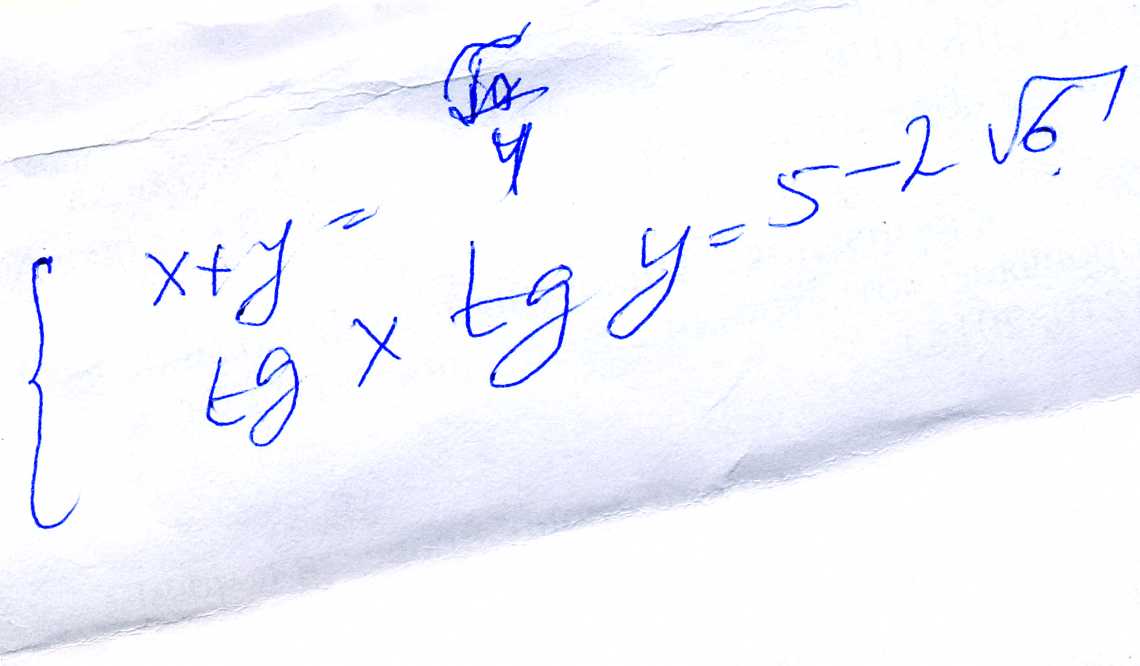
Решение
{tgx*tg((π/4)-x)=5-2sqrt(6)
tg((π/4)-x)=(tg(π/4)-tgx)/(1+tgx*tg(π/4))=(1-tgx)/(1+tgx)
tgx*(1-tgx)/(1+tgx)=5-2sqrt(6);
tgx*(1-tgx)=(5-2sqrt(6))*(1+tgx);
tgx-tg^2x =5-2sqrt(6)+5tgx -2sqrt(6)*tgx
tg^2x+(4-2sqrt(6))tgx +(5-2sqrt(6))=0
D=(4-2sqrt(6))^2-4*(5-2sqrt(6))=16-16sqrt(6)+24-20+8sqrt(6)=
=20 -8sqrt(6)=4*(5-2sqrt(6))
tgx=2-sqrt(6)-sqrt(5-2sqrt(6)) или tgx = 2-sqrt(6)+sqrt(5-2sqrt(6))
x_(1) =arctg(2-sqrt(6)-sqrt(5-2sqrt(6)))+πn, n ∈ Z или x_(2)=artctg( 2-sqrt(6)+sqrt(5-2sqrt(6)))+πm, m ∈ Z
y_(1)=( π/4)-arctg(2-sqrt(6)-sqrt(5-2sqrt(6)))-πn, n ∈ Z или y_(2)=( π/4)-arctg(2-sqrt(6)+sqrt(5-2sqrt(6)))-πm, m∈ Z