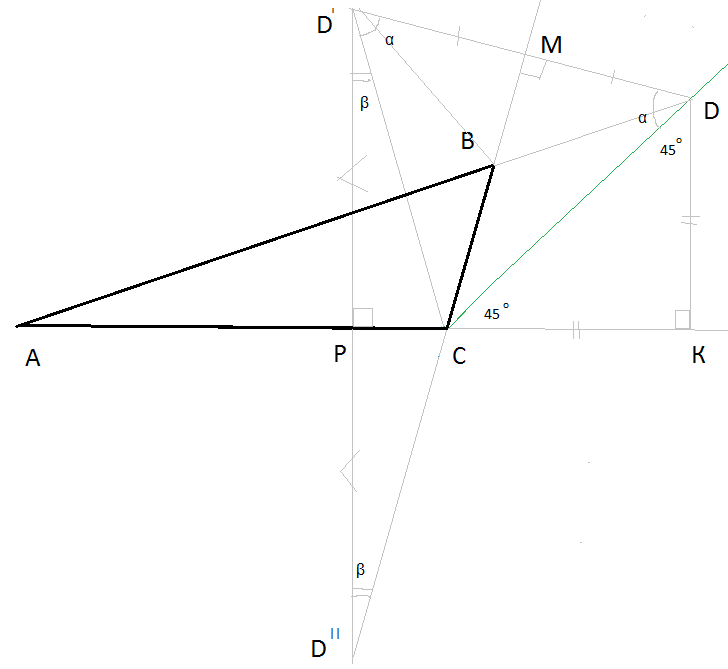
Задача 30576 В треугольнике АВС угол С тупой, а точка...

slava191

2018-10-27 16:59:26

В треугольнике АВС угол С тупой, а точка D выбрана на продолжении АВ за точку В так, что угол ACD = 135 градусов. Точка D' симметрична точке D относительно прямой ВС, точка D'' симметрична точке D' относительно прямой АС и лежит на прямой ВС. Известно, что sqrt(3)*ВС=СD'', AC=6.

А) Докажите, что треугольник CBD - равнобедренный
Б) Найдите площадь треугольника АВС [L16]

sova

2018-10-28 12:59:44

★

Cм. рисунок.
а)
Δ СMD = Δ CMD' по построению симметричной точки D' ⇒
СD=CD'
Δ СPD' = Δ CPD'' по построению симметричной точки D''⇒
СD'=CD''

СD = CD' = CD''

BС - серединный перпендикуляр к DD' ⇒
BD=BD'

Обозначим
∠ СD'D= ∠ CDD'= α
∠ CD'D'' = ∠ CD''D'= β

Проведем DK ⊥ AC;
DK || D'D''
Δ CDK - прямоугольный равнобедренный треугольник.
∠CDK =∠ KСD=45^(o)

PD'DK - прямоугольная трапеция.
Cумма углов, прилежащих к стороне DD' равна 180^(o)
∠CDK +∠ СDD'+ ∠ DD'C+ ∠ CD'D'' =180^(o) ⇒
45^(o)+ α + α + β =180^(o) ⇒
2 α + β =135^(o)

В прямоугольном треугольнике MD'D''
сумма острых углов равна 90 ^(o)

∠ DD'C+ ∠ CD'D'' + ∠ CD''D' =90^(o) ⇒
α + β+β =90^(o)

Решаем систему двух уравнений:
{2 α + β =135^(o)
{α + 2β =90^(o)

Умножаем первое уравнение на 2:
{4α + 2β =270^(o)
{α + 2β =90^(o)

Вычитаем из первого второе
3α=180^(o)
α =60^(o)

Δ СDD' - равносторонний.
BD=BD' ⇒ B - равноудалена от двух вершин равностороннего треугольника, значит равноудалена и от третьей.
BD=BD'=ВС
BD=BC и значит Δ СBD - равнобедренный, что и требовалось доказать.

б) Пусть BC=x, тогда из условия задачи СD'' = x*sqrt(3)
так как в а) получено СD = CD' = CD'', то
СD= x*sqrt(3)
Так как B - равноудалена от двух вершин равностороннего Δ СDD', то BD и ВС - биссектрисы ∠ СDD' и ∠ DСD'

Значит в треугольнике АВС:
∠ АВС=60 ^(o);
∠ АСВ=105^(о)⇒
∠ BAC =15^(o)

По теореме синусов
АС: sin ∠ ABC= BC: sin ∠ BAC

BC=AC*sin15^(o)/sin60^(o)=6*sin15^(o)/(sqrt(3)/2)= 12*sin15^(o)/sqrt(3)

S_( Δ ABC)=(1/2)AC*BC*sin ∠ ACB=

=(1/2)*6*(12*sin15^(о)/sqrt(3))*sin105^(o)=[[b] sin105^(o)=cos15^(o)[/b]]

=(1/2)*6*(12*sin15^(о)/sqrt(3))*cos15^(o)=

=([b]2*sin15^(o)*cos15^(o)=sin30^(o)=1/2[/b])=

=[b]3sqrt(3)[/b]

О т в е т. б) 3sqrt(3)