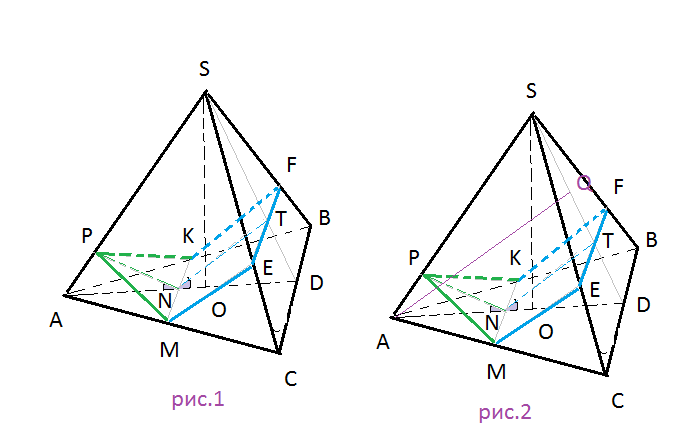
Задача 30574 ...

slava191

2018-10-27 16:54:26

Через середину ребра АС правильной треугольной пирамиды SABC (S - вершина) проведены плоскости α и β , каждая из которых образует угол 30 градусов с плоскостью АВС. Сечения пирамиды этими плоскостями имеют общую сторону длины 1, лежащую в грани АВС, а плоскость α перпендикулярна ребру SA.

А) Найдите площадь сечения пирамиды плоскостью α
Б) Найдите площадь сечения пирамиды плоскостью β [L14]

sova

2018-10-28 21:53:26

★

См. рис. 1
пл. α = пл Δ PKM
пл. β = пл. трапеции KFEM

МК=1
МК - средняя линия Δ АВС
∠ PNA = 30 ^(o)
∠ TND = 30^(o)
SA ⊥ пл. PKM, ∠ SPN=90^(o)

а)
ВС=2MK=2
Δ АВС - равносторонний ⇒ АВ=ВС=АС=2; AD=sqrt(3);
AO=(2/3)AD=2sqrt(3)/3;
OD=(1/3)AD=sqrt(3)/3.

Δ АРN - прямоугольный, ∠ PNA = 30 ^(o); AN=(1/2)AD=sqrt(3)/2
PN=AN*cos30^(o)=3/4

S_( Δ РКМ)=(1/2)*МК*PN=(1/2)*1*(3/4)=3/8
[b]S_(пл. α )=3/8 [/b]

б)
Δ ASО - прямоугольный, ∠ SAO=60^(o) ( это следует из прямоугольного треугольника АРN с острым углом 30^(o))

SA=AO/cos60(o)=(2sqrt(3)/3): (1/2)=4sqrt(3)/3
SO=AO*tg60^(o)=(2sqrt(3)/3)*sqrt(3)=2

Из прямоугольного Δ SDО по теореме Пифагора
SD^2=SO^2+OD^2=2^2+(sqrt(3)/3)^2=13/3

В треугольнике SAD биссектриса AQ || высоте трапеции NT
так как ∠ QAO=∠TND=30^(o) ( односторонние углы равны, прямые параллельны)

По свойству биссектрисы угла треугольника
SQ:QD=SA: AD=(4sqrt(3)/3 ): sqrt(3)=4:3

SQ=(4/7)AQ
QD=(3/7)AQ=sqrt(39)/7

Из AQD по теореме косинусов:
QD^2=AQ^2+AD^2-2AQ*AD*cos30^(o)
Получим квадратное уравнение:
AQ^2-3AQ+(108/49)=0
D=9-4*(108/49)=9/49

AQ=(3 ± (3/7))/2
[b]AQ=24/14=12/7 [/b] или AQ=9/7

NT=(1/2)AQ=[b]6/7[/b] - cредняя линия Δ AQD
QN=ND
и потому

ST:TD=(4+(3/2)):(3/2)=11 : 3

Из подобия Δ SFE и Δ SBC
FE: BC=11:14
FE=11BC/14=11*2/14=11/7

S_(трапеции KFEM)=(MK+FE)*NT/2=(1/2)*(1+(11/7))*(6/7)=54/49

[b]S_(пл β )=54/49[/b]

О т в е т.а) [b]S_(пл. α )=3/8 [/b]; б)[b]S_(пл β )=54/49[/b]