Задача 30440 ...

7gev

22 октября 2018 г. в 17:00

Решите неравенство
4log²₄(sin³x) + 8log₂(sinx) ≥ 1

sova

22 октября 2018 г. в 17:22

★

ОДЗ: sinx >0 ⇒ x ∈ (2πk; π+2πk) , k ∈ Z

так как
log₄(sinx)³=3log₄sinx=3log_2²sinx=(3/2)log₂sinx
log²₄(sinx)³=((3/2)log₂sinx)²=(9/4)log²₂sinx

Замена:
log₂sinx=t

9t²+8t–1 ≥0
D=64²–4·9(–1)=64+36=100
t₁=(–8–10)/18=–1 или t₂= (–8+10)/18=1/9

t ≤ –1 или t ≥ 1/9

log₂sinx ≤ –1 или log₂ sinx ≥ 1/9

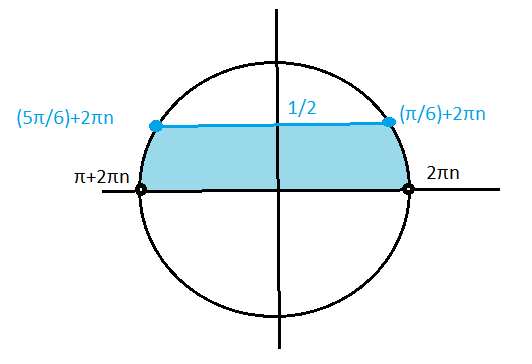
sinx ≤ 1/2 или sinx ≥ 2^1/9 – не имеет решений, 2^1/9 > 1

а |sinx|≤1

C учетом ОДЗ
(2πn;(π/6)+2πn]U[5π/6)+2πn;π+2πn), n ∈ Z