Задача 30390 ...

vk344135258

2018-10-20 22:07:21

Задание 3. Найти интервалы непрерывности функции и точки разрыва. Построить график функции.
3.5. f(x) = { -2(x + 1), x ≤ -1, (x + 1)^3, -1 < x < 0, x, x ≥ 0. }

sova

2018-10-20 22:48:57

★

Функция непрерывна в точке х_(о), если
f(x_(o)-0)=f(x_(o)+0)=f(x_(o))

Две точки исследуем
х= - 1

f(-1 - 0)=lim_(x→-1-0)(-2*(x+1)) =-2*(-1+1)=0
f(-1-0)=-2*(-1+1)=0
f(-1+0)=lim_(x→ -1+0)(x+1)^3=0

x=-1 - точка непрерывности

х=0
f(-0)=lim_(x→-0)(x+1)^3=(+0+1)^3=1
f(0)=0
f(+0)=lim_(x→ +0)x=0

х=0 - точка разрыва первого рода
Есть конечный скачок
1-0=1


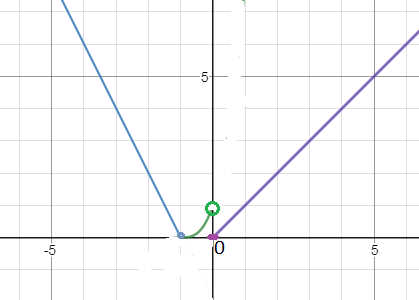
График