Задача 30388 Свести уравнение кривых второго порядка...

leronmarkevich

2018-10-20 18:02:30

Свести уравнение кривых второго порядка к каноническому виду. Найти их фокусы, вершины, директрисы, эксцентриситет.

а) 4x^2+5y^2+8x+10y=0
б) 4x^2-y^2-8x-6y-4=0
в) y=2x^2-12x-9

sova

2018-10-20 22:27:27

★

а) 4x^2+5y^2+8x+10y=0
(4x^2+8x)+(5y^2+10y)=0
4*(x^2+2x)+5*(y^2+2y)=0
4*(x^2+2x+1)-4 + 5*(y^2+2y+1)-5=0
4*(x+1)^2+5*(y+1)^2=9
(x+1)^2/(3/2)^2 + (y+1)^2/(3/sqrt(5))^2=1
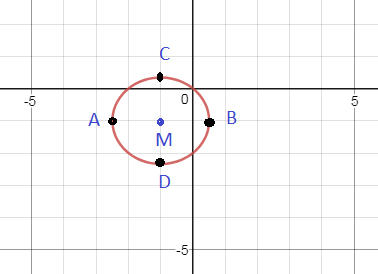
уравнение эллипса c центром в точке M (-1;-1)
фокусы на оси, параллельной оси Ох.

Полуоси:
a=(3/2) и АВ=2а=3
b=(3/sqrt(5)) и СD=2b=6/sqrt(5)
c^2=a^2-b^2=(9/4)-(9/5)=9/20
c=3/(2sqrt(5))
ε=с/a=1/sqrt(5)

cм. рис.1

б) 4x^2–y^2–8x–6y–4=0
(4x^2-8x)-(y^2+6y)-4=0
4*(x^2-2x)-(y^2+6y)-4=0
4(x^2-2x+1)-4-(y^2+6y+9)+9-4=0
4*(x-1)^2-(y+3)^2=-1
((x-1)/(1/2))^2-(y+3)^2= - 1
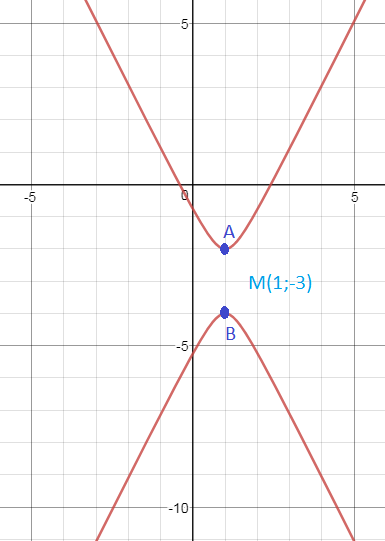
уравнение гиперболы с центром в (1;-3)
фокусы на оси параллельной оси Оу.

Полуоси
a=1 и AB=2
b=1/2
a^2=c^2-b^2
c^2=1-(1/2)^2=3/4
с=sqrt(3)/2

ε=c/b=sqrt(3)

см. рис. 2

в) y=2x^2–12x–9
y=2*(x^2-6x+9)-18-9
y=2*(x-3)^2-27
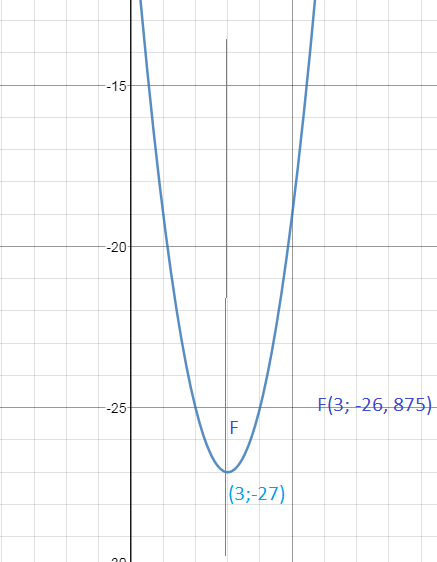
парабола, вершина в точке (3;-27)
2p=1/2
p=1/4

фокус F(3;-27+(1/8))

Уравнение директрисы:

y=27+(1/8)
y=27,125
cм. рис.3