Задача 30282 помогитееее...
Условие
Решение
Область определения
(- ∞ ;4)U(4;+ ∞ )
Функция монотонно возрастает на (- ∞ ;4) и на (4;+ ∞ ),
ее графиком является гипербола
Значит каждое свое значение функция принимает только один раз . Поэтому обратима ( каждому х свой у и обратно каждому у свой х)
Меняем х и у местами
x=(4+y)/(4-y) ⇒
4x-xy=4+y
4x-4=xy+y
4x-4=y*(x+1)
y=(4x-4)/(x+1) - обратная
Область определения:
(- ∞ ;-1)U(-1;+ ∞ )
5б)
Область определения:
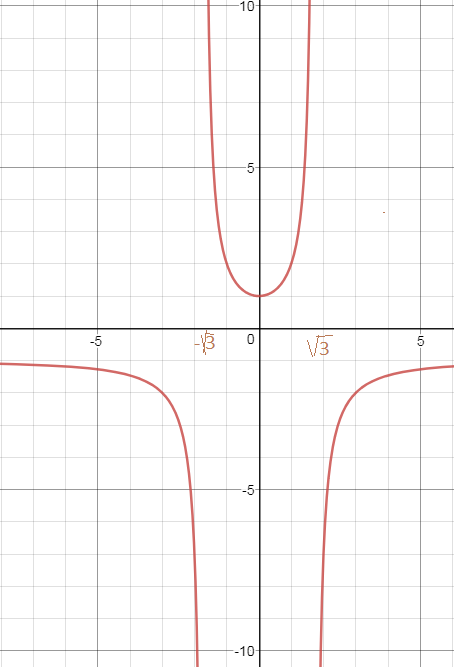
(- ∞ ;-sqrt(3))U(-sqrt(3);sqrt(3))U(sqrt(3);+ ∞ )
функция монотонна на ( см график красного цвета )
на (- ∞ ;-sqrt(3))U(-sqrt(3);0)
и
на [0;sqrt(3))U(sqrt(3);+ ∞ )
Меняем x и y местами
x=(3+y^2)/(3-y^2)
3x-xy^2=3+y^2
3x-3=y^2*(x+1)
y^2=(3x-3)/(x+1) - обратная к данной.
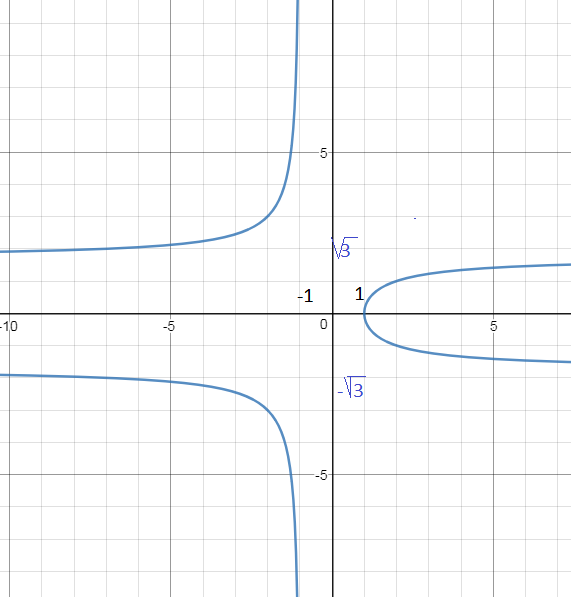
Состоит из двух ветвей ( cм график синего цвета)
y= - sqrt((3x-3)/(x+1)) и y=sqrt((3x-3)/(x+1))
Область определения определяется неравенством
(3x-3)/(x-1) ≥ 0 ⇒ x ∈ (- ∞ ;-1) U(1;+ ∞ )
Синяя кривая вообще говоря не является графиком функции, потому что одному и тому же х ( например, х=5) cоответствует два у.
Поэтому за обратную функцию берут либо
y= - sqrt((3x-3)/(x+1))
(та часть кривой, которая на графике ниже оси Ох)
либо
y=sqrt((3x-3)/(x+1))
(та часть кривой, которая на графике выше оси Ох)
