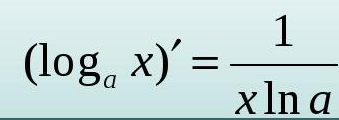Задача 30214 Наибольшее значение y=sqrt(2lgx-1)-lgx...

slava191

2018-10-14 13:26:56

Наибольшее значение y=sqrt(2lgx-1)-lgx

sova

2018-10-14 17:43:29

★

Область определения функции:
{2lgx-1 ≥ 0 ⇒ lgx ≥ 1/2 ⇒ x ≥ sqrt(10)
{x>0

х ∈ [sqrt(10);+ ∞ )

y`=(sqrt(2lgx - 1) - lgx)` = (1/(2sqrt(2lgx-1))) *(2lgx-1)` - (1/x)*(1/ln10)=

=(1-sqrt(2lgx-1))/(x*lg10*sqrt(2lgx-1))

y`=0

1-sqrt(2lgx-1)=0 ⇒ sqrt(2lgx-1)=1 ⇒

2lgx-1=1
2lgx=2
lgx=1
x=10

Производная не существует при х=0 и 2lgx-1=0 ⇒ x=sqrt(10)
0 ∈ ОДЗ
x=sqrt(10) - крайняя левая точка ОДЗ

Исследуем точку х=10 на экстремум

(sqrt(10)) __+__ (10) _____-____

x=10 - точка максимума, производная при переходе через точку меняет знак с + на -

y(10)=sqrt(2*lg10) - lg10=sqrt(2*1-1)-1=0

О т в е т. 0