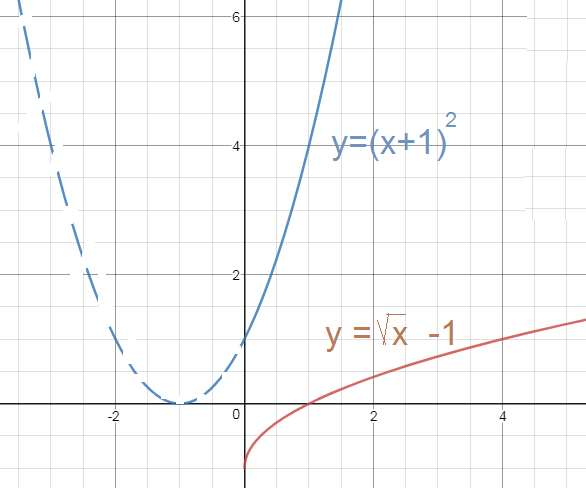Задача 30190 Все кроме третьего, а если понимаете что...
Условие

Решение
a)
Область определения D(y)=(- ∞;-1) U(-1;+ ∞ ).
Множество значений E(y)=(- ∞;0) U(0;+ ∞ ).
Функция не имеет нулей:
Область определения D(y)=(- ∞;-1) U(-1;+ ∞ ).
Множество значений E(y)=(- ∞;0) U(0;+ ∞ )
Функция не имеет нулей
Уравнение y=0
1/(x+1) = 0 не имеет корней.
Кривая y=1/(x+1) не пересекает ось Ох
b)
Область определения D(y)=(- ∞;-1) U(-1;+ ∞ ).
Множество значений E(y)= (- ∞;+ ∞ ).
Нули функции:
(х+2)/(х^3+1)=0
x+2=0
x=-2
Кривая y=(x+2)/(x^3+1) пересекает ось Ох в точке (-2;0)
с) Область определения D(y)=(- ∞;+ ∞ ).
Множество значений E(y)= (0;+ ∞ ).
Нулей функции нет:
e^(2x)=0 - уравнение не имеет корней, e^(2x) > 0 при любом х
d)
Область определения:
2x+1 > 0 ⇒ x> -1/2
D(y)=(-1/2;+ ∞ ).
Множество значений E(y)= (- ∞;+ ∞ ).
Нули функции:
ln(2x+1)=0
2x+1=e^(0)
2x+1=1
2x=0
x=0
Кривая пересекает ось Ох в точке (0;0)
e)
Область определения:
{x+1 > 0 ⇒ x> -1
{x> 0 ⇒ x > 0
D(y)=(0;+ ∞ ).
Множество значений E(y)= (- ∞;+ ∞ ).
Нули функции:
ln(x+1)+lnx=0
ln(x+1)*x=0
(x+1)*x=e^(0)
x^2+x-1=0
В=1-4*(-1)=5
x=(-1-sqrt(5))/2 или x=(-1+sqrt(5))/2
Кривая пересекает ось Ох в двух точках
((-1-sqrt(5))/2 ;0) и ((-1+sqrt(5))/2;0)
f)
Область определения D(y)=(- ∞;+ ∞ ).
Множество значений E(y)= (-∞;+ ∞ ).
Нулb функции :
3e^(-x)-e^(2x)=0
3e^(-x)=e^(2x)
3=e^(3x)
3x=ln3
x=(ln3)/3
2
Определение.
Функция называется четной ( нечетной), если
1) eё область определения симметрична относительно 0
2) и для любого х из области определения выполняется равенство
f(-x)=f(x) для чётности
и соответственно
f(-x)=-f(x) для нечётности
а)
область определения (-∞ ; + ∞ ) - симметрична относительно 0
y(-x)= (-x)^3-(-x)/((-x)^5+(-x)^3))=(-x^3+x)/(-x^5-x^3)=(x^3-x)/(x^5+x^3)=y(x)
функция чётная
b)
область определения (-∞ ; + ∞ ) - симметрична относительно 0
y(-x)= (-x)^2+2))/((-x)^3+(-x)))=(x^2+2)/(-x^3-x)=-(x^2+2)/(x^3+x)=-y(x)
функция нечётная
c) область определения (-∞ ; + ∞ ) - симметрична относительно 0
y(-x)=(-х)+sin(-x)=-x-sinx=-(x+sinx)=-y(x)
функция нечётная
d) область определения (-∞ ; + ∞ ) - симметрична относительно 0
y(-x)=(-х)*cos(-x)=-x*cosx=-(x*cosx)=-y(x)
функция нечётная
e) область определения не содержит точек, в которых
cosx ≠ 0
x ≠ (π/2)+πk, k ∈ Z
область определения симметрична относительно 0
y(-x)=(-х)*sin(-x)/cos(-x)=-x*(-sinx)/cosx=(x*sinx/cosx)=y(x)
функция чётная
3
Функция y=sqrt(x) - 1 для x ≥ 0 монотонно возрастает, значит каждое свое значение принимает ровно один раз. Поэтому обратима. Значит, существует обратная.
Меняем местами х и у
х=sqrt(y)-1
x+1=sqrt(y)
(x+1)^2=y - график парабола, только та часть, которая при x ≥ 0
См. рис.
(то, что синим пунктиром отмечено можно вообще стереть)
4
a)
Составляем обратную
x=2*(1-y^(5/4)^(1/7)
x^7=2^7*(1-y^(5/4))
1-y^(5/4)=(x/2)^7
y^(5/4)=1-(x/2)^7
y=(1-(x/2)^7)^(4/5) - обратная
b)
x=y^2+4y+4
y^2+4y+4-x=0
D=16-4*(4-x)=4x
y=(-4-sqrt(4x))/2 или y=(-4+sqrt(4x))/2
y=-2-sqrt(x) или y=-2+sqrt(x)
две ветви.
с)
x=3*lny^2
(x/3)=lny^2
y^2=e(x/3) - обратная
d)
x=∛e^(y)
x^3=e^(y)
ln(x^3)=y - обратная