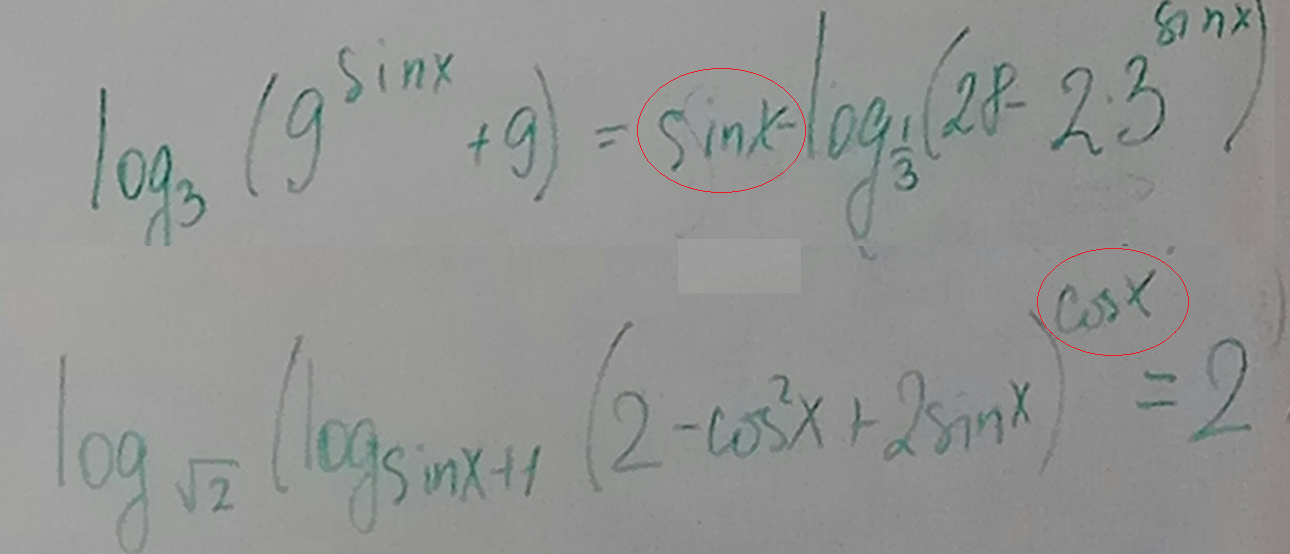Задача 30148 ...
Условие
6 + log_2 (4 cos x) log_2 (16 sin^2 x) = log_2 (64 cos^3 x) + log_2 (256 sin^4 x)
log_√2 (log_sin x+1 (2-cos^3 x+2 sin x)^cos x) =2^7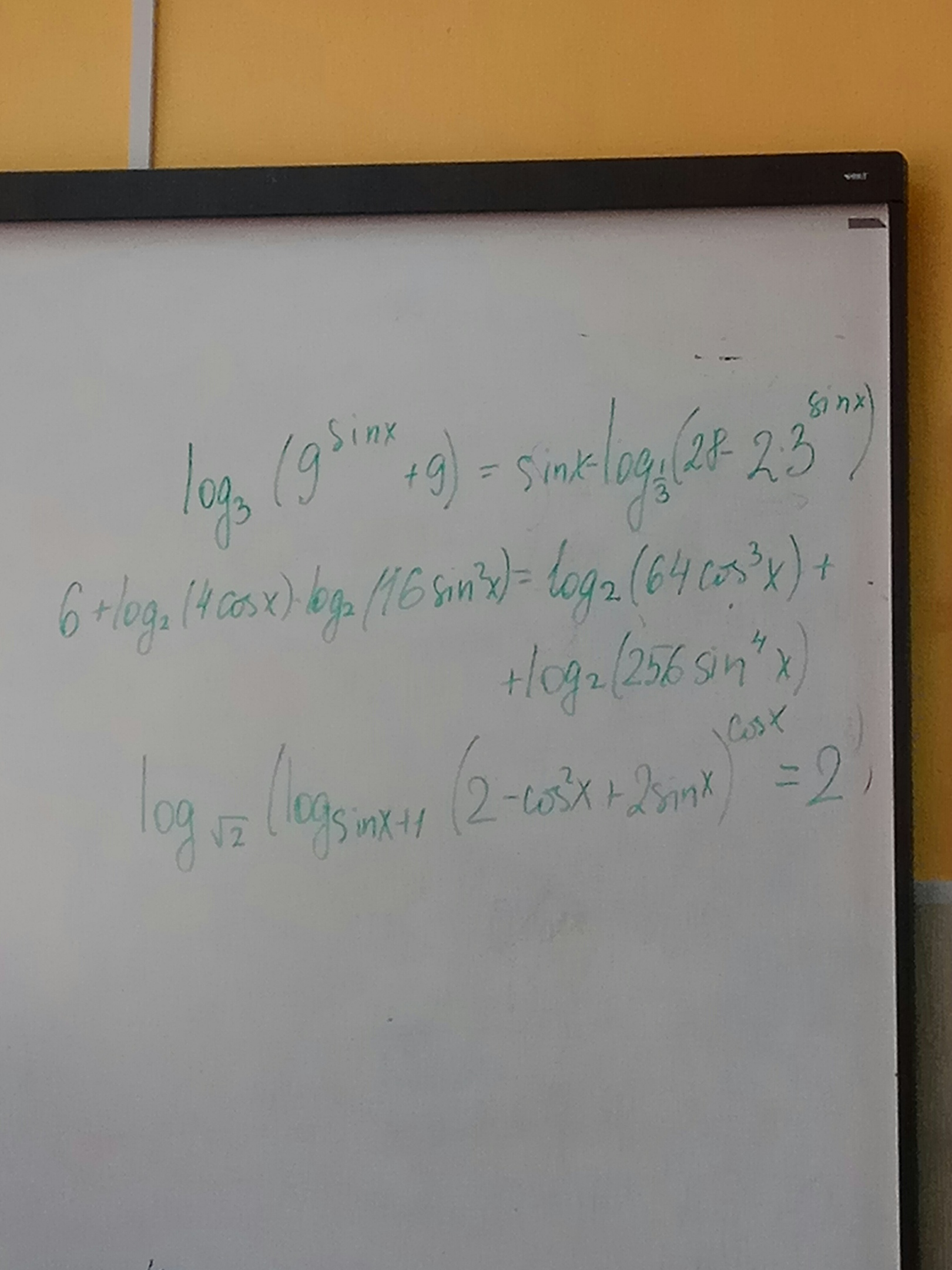
Все решения
2) ОДЗ:
{cosx > 0
{sin^2x>0 ⇒ sinx ≠ 0
log_(2)(4cosx)=log_(2)4+log_(2)cosx
log_(2)(16sin^2x)=log_(2)16+log_(2)sin^2x
log_(2)(64cos^3x)=log_(2)64+log_(2)cos^3x=6+3log_(2)x
log_(2)(256sin^4x)=log_(2)256+log_(2)(sin^2x)^2=
=8+2log_(2)sin^2x
Уравнение принимает вид:
6 + (2+log_(2)cosx)*(4+log_(2)sin^2x)=6+3log_(2)cosx+8+2log_(2)sin^2x;
Раскрываем скобки и приводим подобные слагаемые.
6+8+4log_(2)cosx+2log_(2)sin^2x+log_(2)cosx*log_(2)sin^2x=6+8+3log_(2)cosx+2log_(2)sin^2x;
4log_(2)cosx-3log_(2)cosx+log_(2)cosx*log_(2)sin^2x=0
log_(2)cosx+log_(2)cosx*log_(2)sin^2x=0
log_(2)cosx*(1+log_(2)sin^2x)=0
log_(2)cosx=0 ИЛИ (1+log_(2)sin^2x)=0
1)
log_(2)cosx=0 ⇒ cosx=1 ⇒ x=2πn, n ∈ Z
2)1+log_(2)sin^2x=0 ⇒ log_(2)sin^2x = -1 ⇒ sin^2x=2^(-1) ⇒
sin^2x=1/2
sinx=sqrt(2)/2 или sinx=-sqrt(2)/2
C учетом ОДЗ: сosx >0 ( х в первой или в четвертой четв)
x=(π/4)+2πk, k ∈ Z или х=(-π/4)+2πk, k ∈ Z
О т в е т. 2πn, n ∈ Z; ± (π/4)+2πk, k ∈ Z