Задача 3 Шарик падает на пол с высоты H и...

slava191

Шарик падает на пол с высоты H и многократно отскакивает от него. Полагая, что при каждом отскоке скорость шарика уменьшается в два раза, определить путь, пройденный шариком от начала падения до остановки. Сопротивлением воздуха пренебречь.

1. Скорости шарика после ударов:
- Первая скорость после удара: v_1 = v_0 / n
- Вторая скорость после удара: v_2 = v_1 / n = v_0 / n^2

2. Высоты подъёма после отскоков:
- Первый подъем: h = v_1^2 / (2g) = H^2 / n^2
- Второй подъем: h_2 = v_2^2 / (2g) = H^2 / n^4

3. Общий пройденный путь S:
- S = H + 2(h_1 + h_2 + ...) = H + (2H / n^2) (1 + 1/n^2 + 1/n^4 + ...)

- Сумма геометрической прогрессии: 1 / (1 - 1/n^2) = n^2 / (n^2 - 1)

- Тогда, S = H + 2H / (n^2 - 1); подставляя n = 2,
- S = H((n^2 + 1)/(n^2 - 1)) = H((4 + 1)/(4 - 1)) = H(5/3) = 1.67H.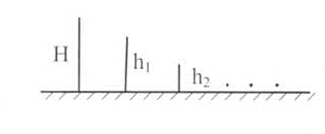

Ответ: 1.67H