Задача 29948 Прямая, проходящая через середину М...

slava191

2018-10-04 17:43:49

Прямая, проходящая через середину М гипотенузы АВ прямоугольного
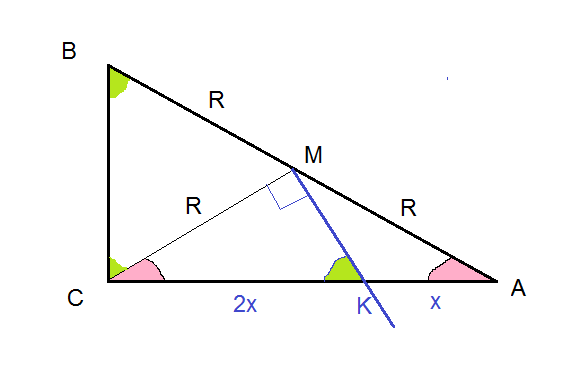
треугольника АВС, перпендикулярна СМ и пересекает
катет АС в точке К. При этом АК : КС =1:2.

а) Докажите, что угол BAC = 30°.

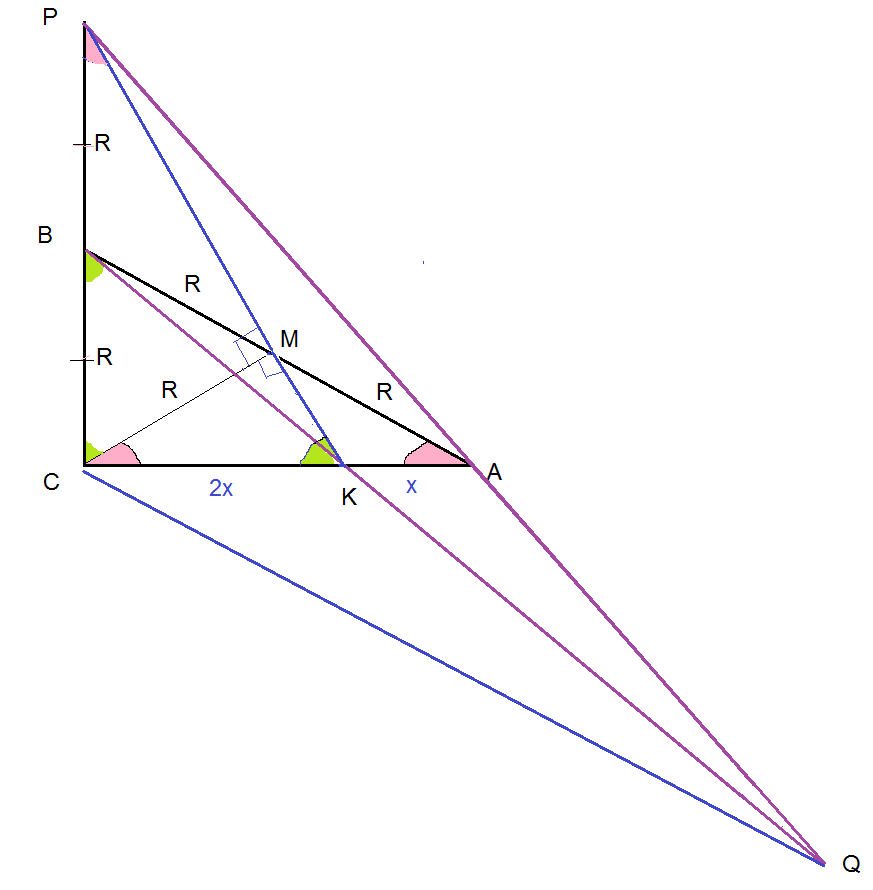
б) Пусть прямые МК и ВС пересекаются в точке Р, а прямые АР и
ВК — в точке Q. Найдите KQ, если ВС = 6sqrt(7) . [v8-16]

sova

2018-10-04 20:53:07

а)
В прямоугольном треугольнике середина гипотенузы - центр описанной окружности.
Пусть
AM=BM=CM=R

Треугольники ВМС и АМС - равнобедренные.
∠МВС=∠ВСМ
∠МСА=∠МАС

Прямоугольные треугольники
АВС и СМК подобны по двум углам.

Из подобия треугольников следует пропорциональность сторон:
АВ : СК = АС : СM

Пусть х - коэффициент пропорциональности.
AK=x
KC=2x

2R : 2x = 3x : R

2R^2=6x^2
R^2=3x^2
R=x*sqrt(3)

сos ∠ BAC=AC/AB=3x/2R=3x/2x*sqrt(3)=sqrt(3)/2 ⇒
∠ BAC = 30 градусов

б)
Δ ВМС - равностороний.
По условию ВС=6sqrt(7)
BC=R

R=6sqrt(7)
x=6sqrt(7)/sqrt(3)=2sqrt(21)

AK=2sqrt(21)
KC=4sqrt(21)

По теореме Пифагора
из прямоугольного треугольника ВСК
ВК^2=BC^2+CK^2=(6sqrt(7))^2+(4sqrt(21))^2=588
BK=sqrt(588)

В прямоугольном треугольнике РСМ
∠ РСМ=60 градусов, значит ∠ СРМ=30 градусов.
Катет против угла в 30 градусов равен половине гипотенузы.
Значит гипотенуза РС=2СM=2R=12sqrt(7)

Т.е. точка В - середина СР.