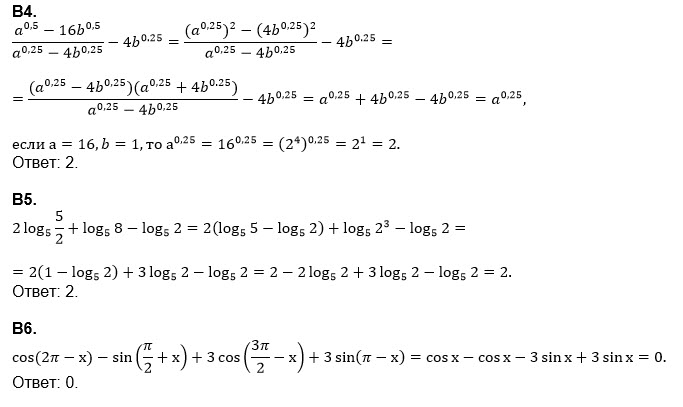Задача 29815 B1. Найдите наибольшее целое число —...

katerug

2018-09-26 21:27:20

B1. Найдите наибольшее целое число — решение неравенства
[m] \frac{36 - x^2}{x} \geq 0. [/m]

B2. Найдите значение выражения
[m] \left( \sqrt[3]{40 - \sqrt{625}} \right) \cdot \sqrt[3]{25} + \sqrt{25} - \sqrt{16}. [/m]

B3. Решите уравнение [m] \log_{\frac{1}{4}}(9 - 5x) = -3. [/m]

B4. Найдите значение выражения
[m] \frac{a^{0,5} - 16b^{0,5}}{a^{0,25} - 4b^{0,25}} = 4b^{0,25}, [/m]

если [m] a = 16, \, b = 1. [/m]

B5. Вычислите:
[m] 2\log_5 \frac{5}{2} + \log_5 8 - \log_5 2. [/m]

6. Упростите выражение
[m] \cos (2\pi - x) - \sin \left( \frac{\pi}{2} + x \right) + 3 \cos \left( \frac{3\pi}{2} - x \right) + 3 \sin (\pi - x). [/m]

При каком значении аргумента [m] x [/m] значение функции
[m] f(x) = 7 \cdot 2^{x - 3} [/m]

равно 28?

Найдите произведение целых чисел — решений неравенства
[m] \log_9 (2x - 4) \geq \log_9 (5 - x). [/m]