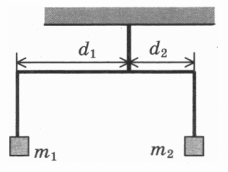
Коромысло весов, к которому подвешены на нитях два тела (см. рисунок), находится в равновесии. При этом плечи коромысла равны d1 = 10 см, d2 = 5 см. Массу первого тела уменьшили в 2 раза. Какой длины нужно сделать плечо чтобы равновесие сохранилось? (Коромысло и нити считать невесомыми, масса второго тела не меняется.) [v1-4]
физика 10-11 класс
38413
Момент, создаваемый первым грузом m1*g*d1 (вращает стержень против часовой стрелке), вторым m2*g*d2 (по часовой). Чтобы стержень находился в равновесии, полный момент всех внешних сил относительно точки подвеса должен быть равен 0.
m1gd1-m2gd2 = 0
m1d1 = m2d2
Отсюда следует мысль, если массу первого тела уменьшили в 2 раза, то [b]плечо d1 надо в 2 раза увеличить (сделать его 20 см)[/b] ИЛИ [b]в 2 раза уменьшить плечо d2 (сделать его 2,5 см)[/b]
