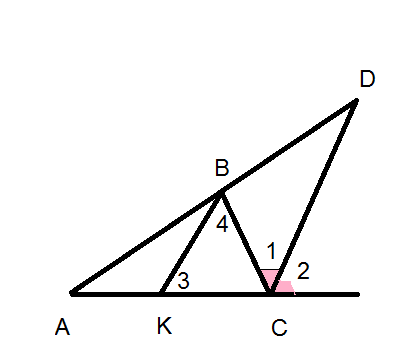
Задача 29735 В треугольнике АВС биссектрисса внешнего...

u21387156141

2018-09-21 19:48:24

В треугольнике АВС биссектрисса внешнего угла при вершине С пересекает прямую АВ в точке D. Доказать, ЧТО AD:BD=AC:BC.

sova

2018-10-03 14:48:09

Проводим BK || CD.

∠ 3= ∠ 2 как соответственные при параллельных прямых BK || CD и секущей АС

∠ 4= ∠ 1 как внутренние накрест лежащие при параллельных прямых BK || CD и секущей ВС

∠ 1= ∠ 2 ( по условию, СD - биссектриса) ⇒ ∠ 3= ∠ 4
Значит, треугольник ВКС - равнобедренный и
ВС=КС

По теореме Фалеса

AD : BD = AC : KC

Заменим КС на ВС и получим требуемое