Задача 29676 (log9x-log(18)x)/(log(18)(2-x)-log(36)(2-x))...

slava191

2018-09-18 01:09:55

(log9x-log(18)x)/(log(18)(2-x)-log(36)(2-x)) меньше или равно log(36)9

sova

2018-10-03 15:34:49

★

ОДЗ:
{x>0
{2-x>0 ⇒ x < 2
{log_(18)(2-x)-log_(36)(2-x)≠0 (cм. преобразования знаменателя ⇒ (2-х)≠1 ⇒х≠1)
[b] x ∈ (0;1)U(1;2) [/b]

Применяем формулу перехода к другому основанию и переходим к основанию 9:

(log_(9)x - (log_(9)x/log_(9)18))/(log_(9)(2-x)/log_(9)18)-(log_(9)(2-x)/log_(9)36) ≤ log_(9)9/log_(9)36;

[b]упрощаем

1) числитель[/b]
log_(9)x - (log_(9)x/log_(9)18)=

=log_(9)x*(log_(9)18 - 1)/(log_(9)18)=

=log_(9)x*(log_(9)18-log_(9)9)/(log_(9)18)=

=log_(9)x*(log_(9)18/9)/(log_(9)18)=

=log_(9)x*(log_(9)2)/(log_(9)18)=


[b] знаменатель [/b]:

(log_(9)(2-x))/(log_(9)18)-(log_(9)(2-x))/(log_(9)36) =

=log_(9)(2-x)*(log_(9)36-log_(9)18)/(log_(9)18*log_(9)36)=

=log_(9)(2-x)*(log_(9)36/18)/(log_(9)18*log_(9)36)=

=log_(9)(2-x)*(log_(9)2)/(log_(9)18*log_(9)36)

Тогда неравенство принимает вид:

log_(9)x*log_(9)36/log_(9)(2-x) ≤ 1/(log_(9)36)

log_(9)x/log_(9)(2-x) ≤ 1/(log^2_(9)36)

Неравенство верно при любом х из области допустимых значений уравнения:

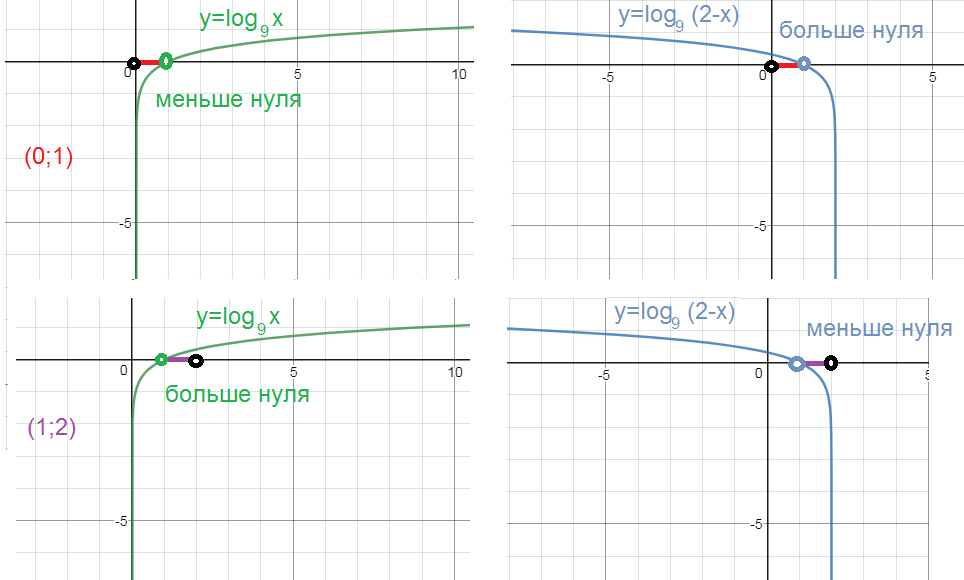
При x ∈ (0,1)
log_(9)x < 0
log_(9)(2-x) > 0
cм. рис.1
При x ∈ (1,2)
log_(9)x > 0
log_(9)(2-x) < 0

log_(9)x/log_(9)(2-x) < 0 при любом х ∈ (0;1)

1/(log^2_(9)36) > 0

О т в е т. (0;1) U (1;2)