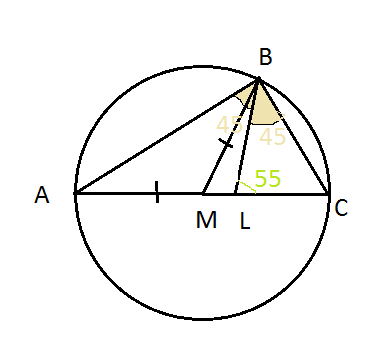
Задача 29544 Найдите углы треугольника АВС , если его...

slava191

2018-09-09 13:04:25

Найдите углы треугольника АВС , если его медиана ВМ равна половине стороны АС , а один из углов, образованных биссектрисой BL и стороной АС, равен 55°. [9.47]

sova

2018-09-09 16:40:16

★

АМ=МС=(1/2)АС ( М - середина АС)

ВМ =(1/2)АС.

Получили АМ=МС=МB , точка М равноудалена от вершин треугольника АВС.
Значит, М - центр описанной около треугольника АВС окружности.

АС - диаметр и значит ∠ ABL=LBC=45 градусов.

Сумма углов треугольника ВLС равна 180 градусов.

∠ ВСА= 180 градусов - ∠ СВL - ∠ BLC=
=180 градусов - 45 градусов - 55 градусов=80 градусов.


∠ ВAC= 90 градусов - ∠ ВCA= 90 градусов - 80 градусов = 10 градусов.

О т в е т. 90 градусов; 80 градусов; 10 градусов.