Задача 29543 ...

slava191

2018-09-09 13:01:58

В треугольнике АВС проведены высота ВН и медиана ВМ . Найдите угол ∠MBH , если АВ = 1, ВС = 2 и AM = ВМ. [9.46]

sova

2018-09-09 15:29:28

★

ВМ - медиана, значит АМ=МС

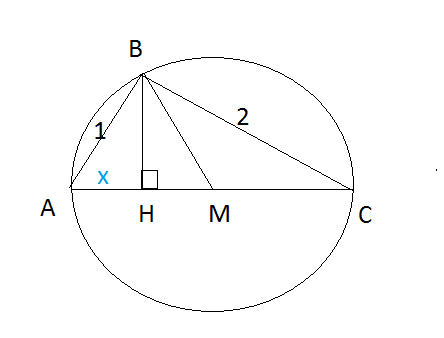
АМ=ВМ по условию

АМ=ВM=MC

Точка М равноудалена от всех вершин треугольника АВС, поэтому
M - центр описанной окружности.

АС - диаметр этой окружности, и ∠ АВС= 90 градусов
По теореме Пифагора
AC^2=AB^2+BC^2
AC^2=1+4=5
AC=sqrt(5)
AM=MC=BM=sqrt(5)/2

Пусть AН=х, тогда из прямоугольного треугольника ABН по теореме Пифагора
BH^2=AB^2-AH^2=1-x^2

Из прямоугольного треугольника ВНС (HC=AC-AH=sqrt(5)-x;

по теореме Пифагора
BH^2=BС^2-HС^2
1 - x^2 = 2^2-(sqrt(5) - x)^2;
1 - x^2 = 4-5 +2 sqrt(5)x -x^2;

x=1/sqrt(5)

BH=sqrt(1-x^2)=sqrt(1-(1/sqrt(5))^2)=sqrt(1-(1/5)=sqrt(4/5)=2/sqrt(5)

Из прямоугольного треугольника МВН

cos ∠ MBH=BH/BM=(2/sqrt(5))/(sqrt(5)/2)=4/5=0,8

∠ MBH=arccos 0,8