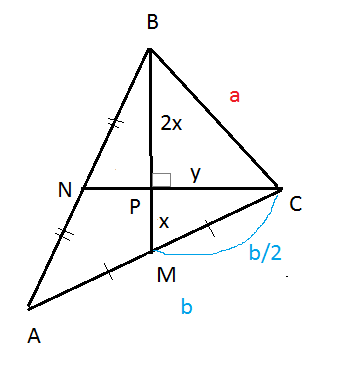
Задача 29542 Медианы ВМ и CN треугольника АВС взаимно...

slava191

2018-09-09 12:49:55

Медианы ВМ и CN треугольника АВС взаимно перпендикулярны. Найдите площадь треугольника АВМ , если ВС = а и АС = b. [9.44]

sova

2018-09-10 09:06:40

★

Пусть медианы ВМ и СN пересекаются в точке P.
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Обозначим
BM=3x, тогда BP=2x; PM=x
CP=y

По теореме Пифагора из прямоугольного треугольника BPC:
(2x)^2+(y)^2=a^2;
По теореме Пифагора из прямоугольного треугольника MPC:
(x)^2+(y)^2=(b/2)^2.

Система уравнений:
{(2x)^2+(y)^2=a^2;
{(x)^2+(y)^2=(b^2)/4.

Вычитаем из первого второе:
3x^2=a^2-(b^2)/4;
x^2=(4a^2-b^2)/12

y^2=(b^2)/4-x^2=(4b^2-4a^2)/12

S( Δ АВМ)=S(BMC), так как АМ=МС, высота общая.

S( Δ BMC)=(1/2)BM*CP=(1/2)*3*x*y=

=(1/2)*3*sqrt((4a^2-b^2)/12)*sqrt(4b^2-4a^2)/12)=

=sqrt(5a^2b^2-a^4-b^4)/4

О т в е т. sqrt(5a^2b^2-a^4-b^4)/4