Задача 29541 ...

slava191

2018-09-09 12:48:37

Через точку К диаметра АВ окружности проведена хорда MN. Найдите А В , если ∠ABM = 30°, ∠BMK = 15° и МК = 3 . [9.43]

sova

2018-09-10 14:30:17

★

∠ANM=∠ABM = 30°,
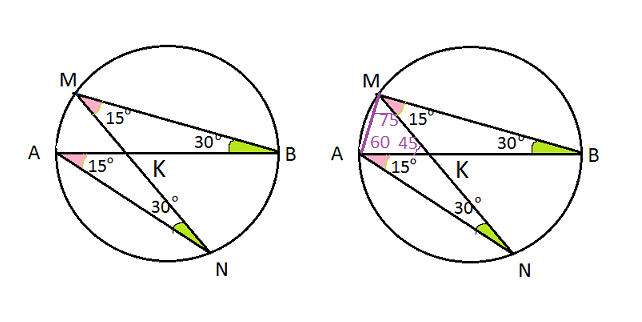
∠NAK=∠BMK = 15°
как углы опирающиеся на одну и ту же дугу

∠ АМВ= 90 °, как угол опирающийся на диаметр АВ

∠ АМК= 90 ° – 15 °= 75 °.

Внешний угол треугольника равен сумме внутренних, с ним не смежных, поэтому

∠ MKA= ∠ BMN + ∠ ABM=

=15 ° + 30 ° = 45 °

∠ МAК= 180 ° – 75 °- 45 °= 60°.

МК=3

По теореме синусов из Δ MAK

MА/sin45° = MK/sin60° ⇒ MA=sqrt(6)

MB=2MA=2sqrt(6) по свойству катета, лежащего в прямоугольном треугольнике против угла в 30 градусов.

По теореме Пифагора

АВ^2=MA^2+MB^2=(sqrt(6))^2+(2sqrt(6))^2=6+24=30

AB= sqrt(30)

О т в е т. MB=2sqrt(6); AB=sqrt(30)