Задача 29538 На диагонали LN параллелограмма KLMN...

slava191

2018-09-09 12:38:14

На диагонали LN параллелограмма KLMN отмены точки Р и Q, причем LP=PQ=QN

А) Докажите, что прямые КР и KQ проходят через середины сторон параллелограмма.

Б) Найдите отношение площади параллелограмма KLMN к площади пятиугольника MRPQS, где R - точка пересечения КР со стороной LM, S - точка пересечения KQ с MN. [Ларин 16]

sova

2018-09-11 00:13:49

Δ KLQ и Δ SNQ подобны по трем углам:
∠ LQK = ∠ NQS как вертикальные,
два других угла как внутренние накрест лежащие при параллельных KL и SN.

Из подобия следует пропорциональность сторон:
SN:LK=QS:KQ=QN=LQ=1:2 ( по условию LP=PQ=QN и значит LQ=2QN)
S_( Δ SNQ) : S_( Δ KLQ)=1:4

Пусть S(параллелограмма KLMN)=[b]S[/b]
S_(Δ KLN)=[b]S[/b]

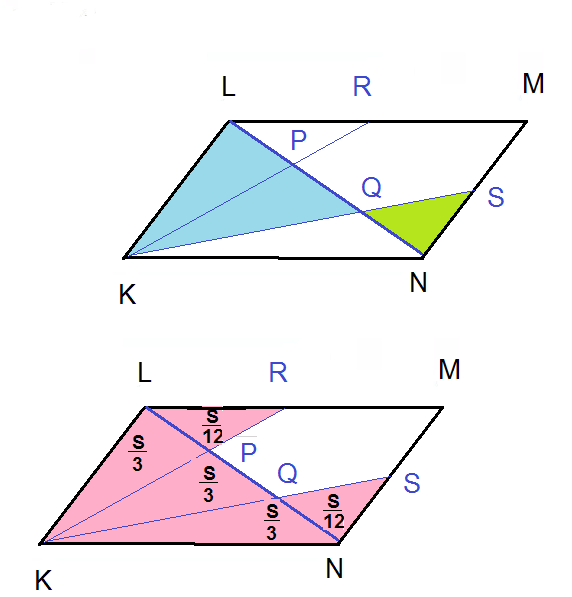
S_( Δ LKP)=S_( Δ KPQ)=S_( Δ KQN)=S_(Δ KLN)/3=([b]S[/b]/6;

S_( Δ SNQ) =S_( Δ KLQ)/4 = 2*([b]S[/b]/6)/4=[b]S[/b]/12;

Аналогично,

S_( Δ LPR)=S_( Δ KPN)/4=[b]S[/b]/12;

S_(MRPQS)=[b]S[/b] - ([b]S[/b]/12)-3*([b]S[/b]/3)-([b]S[/b]/12)=
(cм. рис.2)
=([b]S[/b]/3)

S(параллелограмма KLMN) : S_(MRPQS)=3:1

О т в е т. 3:1