Задача 29536 ...

slava191

2018-09-09 12:24:42

Трапеция ABCD с основаниями ВС = а и AD = b вписана в окружность. Найдите радиус окружности, если ∠ CAD = α . [9.41]

sova

2018-09-09 21:47:29

★

Если трапеция вписана в окружность, то она равнобедренная.
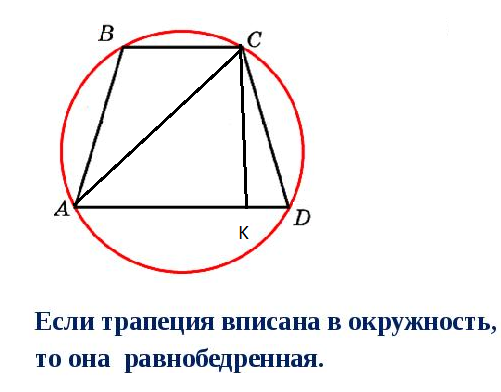
Дуги АВ и СD, заключенные между параллельными хордами ВС и AD равны. Значит и хорды AB и CD равны.

Проводим высоту СК
KD=(b-a)/2
AK=b-(b-a)/2=(a+b)/2

H( трапеции) =СK=AK*cos α = (a+b)cos α /2

Окружность описана не только около трапеции, но и около треугольника ACD.

Поэтому для нахождения радиуса применим формулу

R= AC*CD*AD/4S(Δ ACD)


S ( Δ ACD)=(1/2)AD*CK= (1/2)*b* (a+b)cos α /2=b*(a+b)*cos α /4.

AC^2=AK^2+CK^2=((a+b)/2)^2+((a+b)*(cos α)/2)^2

AC=(a+b)sqrt(1+cos^2α)/2

CD^2=CK^2+KD^2=((a+b)*(cos α)/2)^2+ ((b-a)/2)^2=

=(a^2+b^2)*(1+cos^2 α )/4

CD=sqrt((a^2+b^2)*(1+cos^2 α ))/2

[b]R=((1/cosα)+cosα)*sqrt(a^2+b^2)[/b]