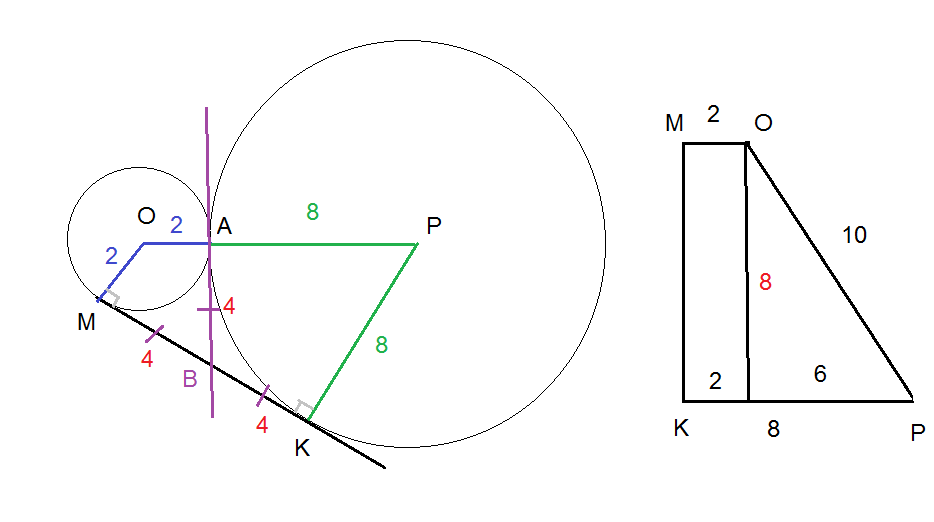
Задача 29532 Две окружности радиусов 2 и 8 касаются...

slava191

2018-09-09 12:18:31

Две окружности радиусов 2 и 8 касаются друг друга внешним образом в точке А. Общая касательная к ним, проведенная через точку А , пересекает другую общую касательную в точке В . Найдите АВ. [9.34.]

sova

2018-09-11 13:20:24

★

Касательная перпендикулярна радиусу, проведённому в точку касания.
OM ⊥ MK
PK ⊥ MK

KOMP - прямоугольная трапеция.
MO=2
KP=8
OP=2+8=10

Проводим высоту из точки О на РК,
получаем прямоугольный треугольник с гипотенузой 10 и катетом
8-2=6
MK=8 ( по теореме Пифагора, египетский треугольник, 10 ; 8 ; 6)

По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны:

ВМ=ВА
ВА=MK

BM=BK=(1/2)MK=4

AB=BM=4

О т в е т. 4