Задача 29529 ...

slava191

2018-09-09 12:07:43

Около треугольника АВС описана окружность с диаметром AD = 2 . Найдите ВС , если АВ = 1 и ∠ BAD : ∠ CAD = 4:3. [9.31]

sova

2018-09-10 19:29:52

★

Δ АОВ - равносторонний:
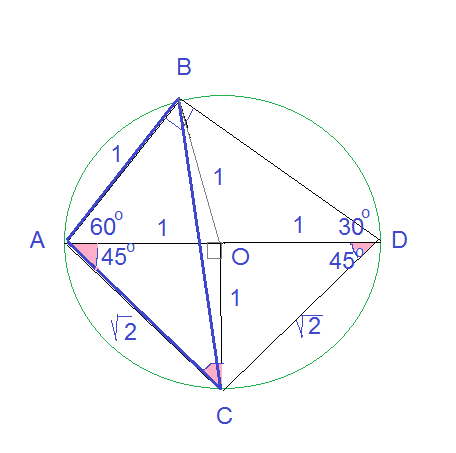
AO=OB=R=1
AB=1 по условию
Значит, ∠ ∠ BAD =60 градусов, ∠ CAD= 45 градусов.

Δ AOC - равнобедренный, (AO=OC=R=1)
∠ CAD=45 градусов, Значит ∠ ACO =45 градусов.
AC=sqrt(2)

[b] Первый способ решения[/b]
По теореме косинусов
BC^2=AB^2+BC^2-2*AB*BC*cos ∠ BAC.

∠ BAC=60 градусов + 45 градусов=105 градусов

сos ∠ BAC=cos105 градусов= сos(60 градусов+ 45 градусов)=

=cos 60 градусов*cos 45 градусов - sin 60 градусов* sin 45 градусов =(sqrt(2)/2)*(1-sqrt(3))/2

BC^2=1+(sqrt(2))^2 -2*1*sqrt(2)*(sqrt(2)/2)*(1-sqrt(3))/2=

=1+2 -1+sqrt(3)=2+sqrt(3)

[b]BC=sqrt(2+sqrt(3))[/b]


[b] Второй способ решения[/b]

По теореме синусов:

BC/sin∠ BAC=2R

sin∠ BAC=sin 105 градусов=sin(60 градусов+ 45 градусов)=

=sin 60 градусов*cos 45 градусов +cos 60 градусов* sin 45 градусов =
=(sqrt(2)/2)*(sqrt(3)+1)/2=sqrt(2)*(sqrt(3)-1)/4

BC=2R*sin105 градусов = 2*(sqrt(2)/2)*((sqrt(3)+1)/2)=

=sqrt(2)*(sqrt(3)+1)/2=(sqrt(6)+sqrt(2))/2

[b]BC=(sqrt(6)+sqrt(2))/2[/b]


Оба ответа равны между собой ( !!!)

sqrt(2+sqrt(3))=(sqrt(6)+sqrt(2))/2

Возводим в квадрат:

2+sqrt(3) =( 6+2sqrt(6)*sqrt(2) + 2)/4 - верно

2+sqrt(3) = 2+sqrt(3)

О т в е т. [b]BC=(sqrt(6)+sqrt(2))/2[/b] или [b]BC=sqrt(2+sqrt(3))[/b]