Задача 29516 16. В трапеции ABCD с основаниями ВС и...
Условие
а) Докажите, что AB=CD;
б) Найдите AD, если АВ=2, BС=7 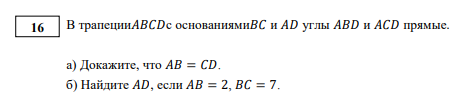
Решение
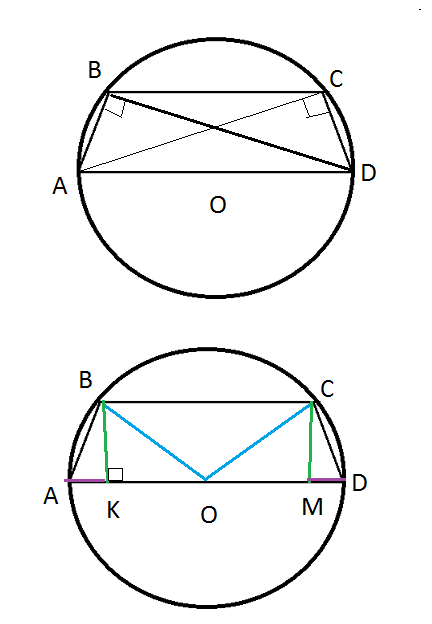
Так как по условию углы ABD и ACD прямые, значит опираются на диаметр и около трапеции АВСD можно описать окружность.
Так как BC|| AD, то дуги заключенные между параллельными прямыми равны.
дуга АВ= дуге CD.
Значит и хорды, стягиваемые этими дугами равны.
АВ=СD.
б) В решении а) доказано, что трапеция АВСD - равнобедренная.
АО=ОD=OB=OC как радиусы описанной окружности.
Проведем высоты ВК и СМ из вершин верхнего основания на нижнее.
АК=MD
KO=OM=(1/2)BC=3,5
Пусть АК=MD=x
АО=х+3,5
Так как BK - катет прямоугольного треугольника АВК, то по теореме Пифагора
[b]BK^2[/b]=AB^2-AK^2
Так как BK - катет прямоугольного треугольника ВКO, то по теореме Пифагора
[b]BK^2[/b]=BO^2-KO^2
Получаем равенство:
AB^2-AK^2=BO^2-KO^2,
подставляя в него
АВ=2; АК=х; ВО=х+3,5; КО=3,5,
получаем уравнение:
2^2-x^2=(x+3,5)^2-3,5^2
4-x^2=(x+3,5-3,5)*(x+3,5+3,5);
4-x^2=x*(x+7)
2x^2+7x-4=0
D=49-4*2*(-4)=81
x=(7+9)/4=4, второй корень уравнения
отрицательный и не удовлетворяет смыслу задачи
AD=2x+7=2*4+7=15
О т в е т б) 15