Задача 29506 9.5. В прямоугольном треугольнике АВС с...
Условие
математика 10-11 класс
11975
Решение
★
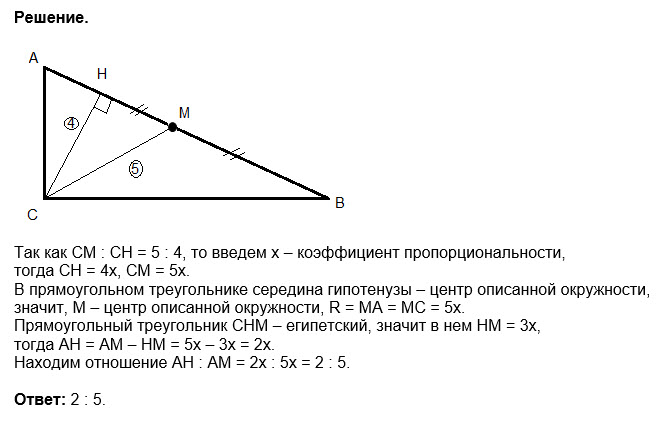
В прямоугольном треугольнике основание медианы, проведенной из прямого угла - центр описанной окружности
АМ=МВ=СМ = R
CM =0,8 CM=0,8*R
Из прямоугольного треугольника СНМ по теореме Пифагора:
НМ^2=CM^2-CH^2
НМ^2=R^2-(0,8R)^2=R^2 -0,64R^2=0,36R^2
HM=0,6R
AH=AM-HM=R-0,6R=0,4R.
AH : AM =0,4R : R=4:10=2:5
О т в е т. 2:5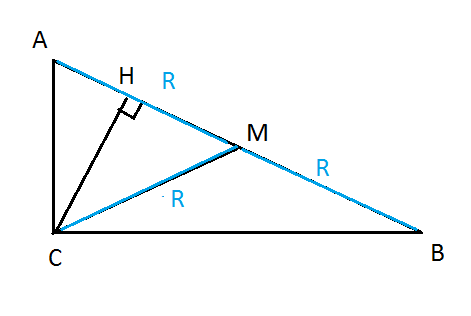
Все решения